
科目: 来源: 题型:
【题目】某公园有一块边长为3百米的正三角形![]() 空地,拟将它分割成面积相等的三个区域,用来种植三种花卉.方案是:先建造一条直道
空地,拟将它分割成面积相等的三个区域,用来种植三种花卉.方案是:先建造一条直道![]() 将
将![]() 分成面积之比为
分成面积之比为![]() 的两部分(点D,E分别在边
的两部分(点D,E分别在边![]() ,
,![]() 上);再取
上);再取![]() 的中点M,建造直道
的中点M,建造直道![]() (如图).设
(如图).设![]() ,
,![]() ,
,![]() (单位:百米).
(单位:百米).
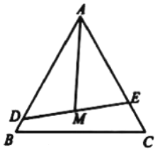
(1)分别求![]() ,
,![]() 关于x的函数关系式;
关于x的函数关系式;
(2)试确定点D的位置,使两条直道的长度之和最小,并求出最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知圆C:
中,已知圆C:![]() ,椭圆E:
,椭圆E:![]() (
(![]() )的右顶点A在圆C上,右准线与圆C相切.
)的右顶点A在圆C上,右准线与圆C相切.
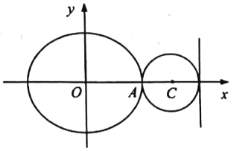
(1)求椭圆E的方程;
(2)设过点A的直线l与圆C相交于另一点M,与椭圆E相交于另一点N.当![]() 时,求直线l的方程.
时,求直线l的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】若函数![]() 在
在![]() 处有极值,且
处有极值,且![]() ,则称
,则称![]() 为函数
为函数![]() 的“F点”.
的“F点”.
(1)设函数![]() (
(![]() ).
).
①当![]() 时,求函数
时,求函数![]() 的极值;
的极值;
②若函数![]() 存在“F点”,求k的值;
存在“F点”,求k的值;
(2)已知函数![]() (a,b,
(a,b,![]() ,
,![]() )存在两个不相等的“F点”
)存在两个不相等的“F点”![]() ,
,![]() ,且
,且![]() ,求a的取值范围.
,求a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了丰富学生的课外文化生活,某中学积极探索开展课外文体活动的新途径及新形式,取得了良好的效果.为了调查学生的学习积极性与参加文体活动是否有关,学校对200名学生做了问卷调查,列联表如下:
参加文体活动 | 不参加文体活动 | 合计 | |
学习积极性高 | 80 | ||
学习积极性不高 | 60 | ||
合计 | 200 |
已知在全部200人中随机抽取1人,抽到学习积极性不高的学生的概率为![]() .
.
(1)请将上面的列联表补充完整;
(2)是否有99.9%的把握认为学习积极性高与参加文体活动有关?请说明你的理由;
(3)若从不参加文体活动的同学中按照分层抽样的方法选取5人,再从所选出的5人中随机选取2人,求至少有1人学习积极性不高的概率.
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
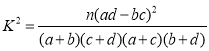 ,其中
,其中![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】在新中国成立70周年国庆阅兵庆典中,众多群众在脸上贴着一颗红心,以此表达对祖国的热爱之情,在数学中,有多种方程都可以表示心型曲线,其中有著名的笛卡尔心型曲线,如图,在直角坐标系中,以原点O为极点,x轴正半轴为极轴建立极坐标系.图中的曲线就是笛卡尔心型曲线,其极坐标方程为![]() (
(![]() ),M为该曲线上的任意一点.
),M为该曲线上的任意一点.
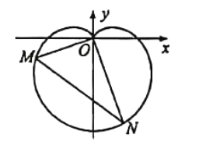
(1)当![]() 时,求M点的极坐标;
时,求M点的极坐标;
(2)将射线OM绕原点O逆时针旋转![]() 与该曲线相交于点N,求
与该曲线相交于点N,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】新型冠状病毒肺炎疫情爆发以来,疫情防控牵挂着所有人的心. 某市积极响应上级部门的号召,通过沿街电子屏、微信公众号等各种渠道对此战“疫”进行了持续、深入的悬窗,帮助全体市民深入了解新冠状病毒,增强战胜疫情的信心. 为了检验大家对新冠状病毒及防控知识的了解程度,该市推出了相关的知识问卷,随机抽取了年龄在15~75岁之间的200人进行调查,并按年龄绘制频率分布直方图如图所示,把年龄落在区间![]() 和
和![]() 内的人分别称为“青少年人”和“中老年人”. 经统计“青少年人”和“中老年人”的人数比为19:21. 其中“青少年人”中有40人对防控的相关知识了解全面,“中老年人”中对防控的相关知识了解全面和不够全面的人数之比是2:1.
内的人分别称为“青少年人”和“中老年人”. 经统计“青少年人”和“中老年人”的人数比为19:21. 其中“青少年人”中有40人对防控的相关知识了解全面,“中老年人”中对防控的相关知识了解全面和不够全面的人数之比是2:1.
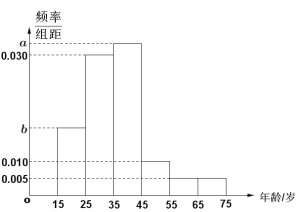
(1)求图中![]() 的值;
的值;
(2)现采取分层抽样在![]() 和
和![]() 中随机抽取8名市民,从8人中任选2人,求2人中至少有1人是“中老年人”的概率是多少?
中随机抽取8名市民,从8人中任选2人,求2人中至少有1人是“中老年人”的概率是多少?
(3)根据已知条件,完成下面的2×2列联表,并根据统计结果判断:能够有99.9%的把握认为“中老年人”比“青少年人”更加了解防控的相关知识?
了解全面 | 了解不全面 | 合计 | |
青少年人 | |||
中老年人 | |||
合计 |
附表及公式: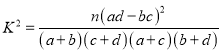 ,其中
,其中![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】三国时代吴国数学家赵爽所注《周髀算经》中给出了勾股定理的绝妙证明.下面是赵爽的弦图及注文,弦图是一个以勾股形之弦为边的正方形,其面积称为弦实.图中包含四个全等的勾股形及一个小正方形,分别涂成红(朱)色及黄色,其面积称为朱实、黄实,利用![]() ,化简,得
,化简,得![]() .设勾股形中勾股比为
.设勾股形中勾股比为![]() ,若向弦图内随机抛掷
,若向弦图内随机抛掷![]() 颗图钉(大小忽略不计),则落在黄色图形内的图钉数大约为( )
颗图钉(大小忽略不计),则落在黄色图形内的图钉数大约为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆E:![]() (
(![]() )的离心率为
)的离心率为![]() ,且短轴的一个端点B与两焦点A,C组成的三角形面积为
,且短轴的一个端点B与两焦点A,C组成的三角形面积为![]() .
.
(Ⅰ)求椭圆E的方程;
(Ⅱ)若点P为椭圆E上的一点,过点P作椭圆E的切线交圆O:![]() 于不同的两点M,N(其中M在N的右侧),求四边形
于不同的两点M,N(其中M在N的右侧),求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知等腰梯形![]() 中(如图1),
中(如图1),![]() ,
,![]() ,
,![]() 为线段
为线段![]() 的中点,
的中点,![]() 、
、![]() 为线段
为线段![]() 上的点,
上的点,![]() ,现将四边形
,现将四边形![]() 沿
沿![]() 折起(如图2)
折起(如图2)
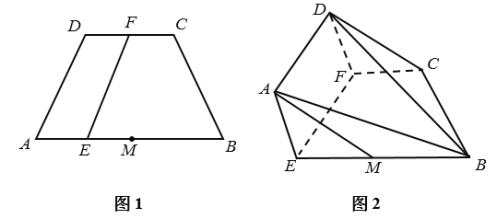
(1)求证:![]() 平面
平面![]() ;
;
(2)在图2中,若![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com