
科目: 来源: 题型:
【题目】某保险公司给年龄在![]() 岁的民众提供某种疾病的一年期医疗保险,现从
岁的民众提供某种疾病的一年期医疗保险,现从![]() 名参保人员中随机抽取
名参保人员中随机抽取![]() 名作为样本进行分析,按年龄段
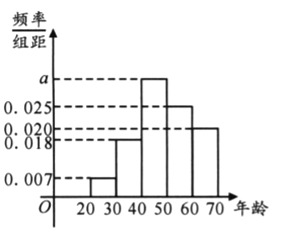
名作为样本进行分析,按年龄段![]() 分成了五组,其频率分布直方图如下图所示;参保年龄与每人每年应交纳的保费如下表所示. 据统计,该公司每年为这一万名参保人员支出的各种费用为一百万元.
分成了五组,其频率分布直方图如下图所示;参保年龄与每人每年应交纳的保费如下表所示. 据统计,该公司每年为这一万名参保人员支出的各种费用为一百万元.
年龄 (单位:岁) |
|
|
|
|
|
保费 (单位:元) |
|
|
|
|
|
(1)用样本的频率分布估计总体分布,为使公司不亏本,求![]() 精确到整数时的最小值
精确到整数时的最小值![]() ;
;
(2)经调查,年龄在![]() 之间老人每
之间老人每![]() 人中有
人中有![]() 人患该项疾病(以此频率作为概率).该病的治疗费为
人患该项疾病(以此频率作为概率).该病的治疗费为![]() 元,如果参保,保险公司补贴治疗费
元,如果参保,保险公司补贴治疗费![]() 元.某老人年龄
元.某老人年龄![]() 岁,若购买该项保险(
岁,若购买该项保险(![]() 取
取![]() 中的
中的![]() ).针对此疾病所支付的费用为
).针对此疾病所支付的费用为![]() 元;若没有购买该项保险,针对此疾病所支付的费用为
元;若没有购买该项保险,针对此疾病所支付的费用为![]() 元.试比较
元.试比较![]() 和
和![]() 的期望值大小,并判断该老人购买此项保险是否划算?
的期望值大小,并判断该老人购买此项保险是否划算?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点A是以BC为直径的圆O上异于B,C的动点,P为平面ABC外一点,且平面PBC⊥平面ABC,BC=3,PB=2![]() ,PC
,PC![]() ,则三棱锥P﹣ABC外接球的表面积为______.
,则三棱锥P﹣ABC外接球的表面积为______.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=ln (x+1)-![]() -x,a∈R.
-x,a∈R.
(1)当a>0时,求函数f(x)的单调区间;
(2)若存在x>0,使f(x)+x+1<-![]() (a∈Z)成立,求a的最小值.
(a∈Z)成立,求a的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】中国古代十进制的算筹计数法,在数学史上是一个伟大的创造,算筹实际上是一根根同长短的小木棍.如图,是利用算筹表示数![]() 的一种方法.例如:3可表示为“
的一种方法.例如:3可表示为“![]() ”,26可表示为“
”,26可表示为“![]() ”.现有6根算筹,据此表示方法,若算筹不能剩余,则可以用
”.现有6根算筹,据此表示方法,若算筹不能剩余,则可以用![]() 这9数字表示两位数的个数为
这9数字表示两位数的个数为![]()
![]()
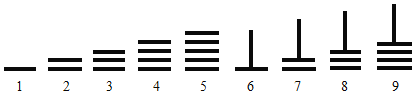
A.13B.14C.15D.16
查看答案和解析>>
科目: 来源: 题型:
【题目】在极坐标系中,点P的坐标是![]() ,曲线C的方程为
,曲线C的方程为![]() .以极点为坐标原点,极轴为x轴的正半轴建立平面直角坐标系,斜率为
.以极点为坐标原点,极轴为x轴的正半轴建立平面直角坐标系,斜率为![]() 的直线l经过点P.
的直线l经过点P.
(1)写出直线l的参数方程和曲线C的直角坐标方程;
(2)若直线l和曲线C相交于两点A,B,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四棱锥P一ABCD中,AB=AD=2BC=2,BC∥AD,AB⊥AD,△PBD为正三角形.且PA=2![]() .
.
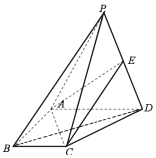
(1)证明:平面PAB⊥平面PBC;
(2)若点P到底面ABCD的距离为2,E是线段PD上一点,且PB∥平面ACE,求四面体A-CDE的体积.
查看答案和解析>>
科目: 来源: 题型:
【题目】小张举办了一次抽奖活动.顾客花费3元钱可获得一次抽奖机会.每次抽奖时,顾客从装有1个黑球,3个红球和6个白球(除颜色外其他都相同)的不透明的袋子中依次不放回地摸出3个球,根据摸出的球的颜色情况进行兑奖.顾客中一等奖,二等奖,三等奖,四等奖时分别可领取的奖金为![]() 元,10元,5元,1元.若经营者小张将顾客摸出的3个球的颜色分成以下五种情况:
元,10元,5元,1元.若经营者小张将顾客摸出的3个球的颜色分成以下五种情况:![]() 个黑球2个红球;
个黑球2个红球;![]() 个红球;
个红球;![]() 恰有1个白球;
恰有1个白球;![]() 恰有2个白球;
恰有2个白球;![]() 个白球,且小张计划将五种情况按发生的机会从小到大的顺序分别对应中一等奖,中二等奖,中三等奖,中四等奖,不中奖.
个白球,且小张计划将五种情况按发生的机会从小到大的顺序分别对应中一等奖,中二等奖,中三等奖,中四等奖,不中奖.
(1)通过计算写出中一至四等奖分别对应的情况(写出字母即可);
(2)已知顾客摸出的第一个球是红球,求他获得二等奖的概率;
(3)设顾客抽一次奖小张获利![]() 元,求变量
元,求变量![]() 的分布列;若小张不打算在活动中亏本,求
的分布列;若小张不打算在活动中亏本,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() 为
为![]() 上位于第一象限的任意一点,过点
上位于第一象限的任意一点,过点![]() 的直线
的直线![]() 交
交![]() 于另一点
于另一点![]() ,交
,交![]() 轴的正半轴于点
轴的正半轴于点![]() .
.
(1)若当点![]() 的横坐标为
的横坐标为![]() ,且
,且![]() 为等腰三角形,求
为等腰三角形,求![]() 的方程;
的方程;
(2)对于(1)中求出的抛物线![]() ,若点
,若点![]() ,记点
,记点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() 交
交![]() 轴于点
轴于点![]() ,且
,且![]() ,求证:点
,求证:点![]() 的坐标为
的坐标为![]() ,并求点
,并求点![]() 到直线
到直线![]() 的距离
的距离![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】某运动制衣品牌为了成衣尺寸更精准,现选择15名志愿者,对其身高和臂展进行测量(单位:厘米),左图为选取的15名志愿者身高与臂展的折线图,右图为身高与臂展所对应的散点图,并求得其回归方程为![]() ,以下结论中不正确的为
,以下结论中不正确的为


A. 15名志愿者身高的极差小于臂展的极差
B. 15名志愿者身高和臂展成正相关关系,
C. 可估计身高为190厘米的人臂展大约为189.65厘米,
D. 身高相差10厘米的两人臂展都相差11.6厘米,
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com