
科目: 来源: 题型:
【题目】新冠肺炎疫情这只“黑天鹅”的出现,给经济运行带来明显影响,住宿餐饮、文体娱乐、交通运输、旅游等行业受疫情影响严重.随着复工复产的有序推动,我市某西餐厅推出线上促销活动:
A套餐(在下列食品中6选3)
西式面点:蔓越莓核桃包、南瓜芝土包、黑列巴、全麦吐司;
中式面点:豆包、桂花糕
B套餐:酱牛肉、老味烧鸡熟食类组合.
复工复产后某一周两种套餐的日销售量(单位:份)如下:
星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 | |
A套餐 | 11 | 12 | 14 | 18 | 22 | 19 | 23 |
B套餐 | 6 | 13 | 15 | 15 | 37 | 20 | 41 |
(1)根据上面一周的销量,计算A套餐和B套餐的平均销量和方差,并根据所得数据评价两种套餐的销售情况;
(2)若某顾客购买一份A套餐,求他所选的面点中至少一种中式面点的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】随着国内疫情形势好转,暂停的中国正在重启,为了尽快提升经济、吸引顾客,哈西某商场举办购物抽奖活动,凡当日购物满1000元的顾客,可参加抽奖,规则如下:盒中有大小质地均相同5个球,其中2个红球和3个白球,不放回地依次摸出2个球,若在第一次和第二次均摸到红球则获得特等奖,否则获得纪念奖,则顾客获得特等奖的概率是_________________.
查看答案和解析>>
科目: 来源: 题型:
【题目】“新冠肺炎”疫情的控制需要根据大数据进行分析,并有针对性的采取措施.下图是甲、乙两个省份从2月7日到2月13日一周内的新增“新冠肺炎”确诊人数的折线图.根据图中甲、乙两省的数字特征进行比对,下列说法错误的是( )

A.2月7日到2月13日甲省的平均新增“新冠肺炎”确诊人数低于乙省
B.2月7日到2月13日甲省的单日新增“新冠肺炎”确诊人数最大值小于乙省
C.2月7日到2月13日乙省相对甲省的新增“新冠甲省肺炎”确诊人数的波动大
D.后四日(2月10日至13日)乙省每日新增“新冠肺炎”确诊人数均比甲省多
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的长轴长为
的长轴长为![]() ,且离心率为
,且离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设椭圆![]() 的左焦点为
的左焦点为![]() ,点
,点![]() 是椭圆与
是椭圆与![]() 轴负半轴的交点,经过
轴负半轴的交点,经过![]() 的直线
的直线![]() 与椭圆交于点
与椭圆交于点![]() ,经过
,经过![]() 且与
且与![]() 平行的直线与椭圆交于点
平行的直线与椭圆交于点![]() ,若
,若![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() ,将
,将![]() 的图像向右平移
的图像向右平移![]() 个单位后,再保持纵坐标不变,横坐标变为原来的2倍,得到函数
个单位后,再保持纵坐标不变,横坐标变为原来的2倍,得到函数![]() 的图象.
的图象.
(1)求函数![]() 在
在![]() 上的值域及单调递增区间;
上的值域及单调递增区间;
(2)若![]() ,且
,且![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】交通安全法有规定:机动车行经人行横道时,应当减速行驶;遇行人正在通过人行横道,应当停车让行.机动车行经没有交通信号的道路时,遇行人横过马路,应当避让.我们将符合这条规定的称为“礼让斑马线”,不符合这条规定的称为“不礼让斑马线”.下表是六安市某十字路口监控设备所抓拍的5个月内驾驶员“不礼让斑马线”行为的统计数据:
月份 | 1 | 2 | 3 | 4 | 5 |
“不礼让斑马线”的驾驶员人数 | 120 | 105 | 100 | 85 | 90 |
(1)根据表中所给的5个月的数据,可用线性回归模型拟合![]() 与
与![]() 的关系,请用相关系数加以说明;
的关系,请用相关系数加以说明;
(2)求“不礼让斑马线”的驾驶员人数![]() 关于月份
关于月份![]() 之间的线性回归方程;
之间的线性回归方程;
(3)若从4,5月份“不礼让斑马线”的驾驶员中分别选取4人和2人,再从所选取的6人中任意抽取2人进行交规调查,求抽取的2人分别来自两个月份的概率;
参考公式:线性回归方程![]() ,其中
,其中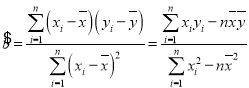 ,
,![]() ,
, .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() :
:![]() (
(![]() 为参数,
为参数,![]() ),曲线
),曲线![]() :
:![]() (
(![]() 为参数),
为参数),![]() 与
与![]() 相切于点
相切于点![]() ,以坐标原点为极点,
,以坐标原点为极点,![]() 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(1)求![]() 的极坐标方程及点
的极坐标方程及点![]() 的极坐标;
的极坐标;
(2)已知直线![]() :
:![]() 与圆
与圆![]() :
:![]() 交于
交于![]() ,
,![]() 两点,记
两点,记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为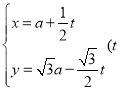 为参数,
为参数,![]() .在以坐标原点为极点、x轴的非负半轴为极轴的极坐标系中,曲线
.在以坐标原点为极点、x轴的非负半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若点![]() 在直线
在直线![]() 上,求直线
上,求直线![]() 的极坐标方程;
的极坐标方程;
(2)已知![]() ,若点
,若点![]() 在直线
在直线![]() 上,点
上,点![]() 在曲线
在曲线![]() 上,且
上,且![]() 的最小值为
的最小值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】函数f(x)=Asin(x+)(A>0,>0,0<<)的部分图象如图所示,又函数g(x)=f(x+![]() ).
).
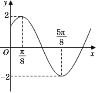
(1)求函数g(x)的单调增区间;
(2)设![]() ABC的内角ABC的对边分别为abc,又c=
ABC的内角ABC的对边分别为abc,又c=![]() ,且锐角C满足g(C)= -1,若sinB=2sinA,,求ABC的面积.
,且锐角C满足g(C)= -1,若sinB=2sinA,,求ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com