
科目: 来源: 题型:
【题目】中国古代的四书是指:《大学》、《中庸》、《论语》、《孟子》,甲、乙、丙、丁![]() 名同学从中各选一书进行研读,已知四人选取的书恰好互不相同,且甲没有选《中庸》,乙和丙都没有选《论语》,则
名同学从中各选一书进行研读,已知四人选取的书恰好互不相同,且甲没有选《中庸》,乙和丙都没有选《论语》,则![]() 名同学所有可能的选择有______种.
名同学所有可能的选择有______种.
查看答案和解析>>
科目: 来源: 题型:
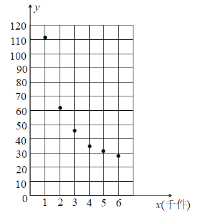
【题目】2020年初全球爆发了新冠肺炎疫情,为了防控疫情,某医疗科研团队攻坚克难研发出一种新型防疫产品,该产品的成本由原料成本及非原料成本组成,每件产品的非原料成本y(元)与生产该产品的数量x(千件)有关,根据已经生产的统计数据,绘制了如下的散点图.
观察散点图,两个变量不具有线性相关关系,现考虑用函数![]() 对两个变量的关系进行拟合.参考数据(其中
对两个变量的关系进行拟合.参考数据(其中![]() ):
):
|
|
|
|
|
|
|
0.41 | 0.1681 | 1.492 | 306 | 20858.44 | 173.8 | 50.39 |
(1)求y关于x的回归方程,并求y关于u的相关系数(精确到0.01).
(2)该产品采取订单生产模式(根据订单数量进行生产,即产品全部售出).根据市场调研数据,若该产品单价定为80元,则签订9千件订单的概率为0.7,签订10千件订单的概率为0.3;若单价定为70元,则签订10千件订单的概率为0.3,签订11千件订单的概率为0.7.已知每件产品的原料成本为30元,根据(1)的结果,要想获得更高利润,产品单价应选择80元还是70元,请说明理由.
参考公式:对于一组数据![]() ,
,![]() ,…,
,…,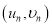 ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: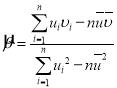 ,
,![]() ,相关系数
,相关系数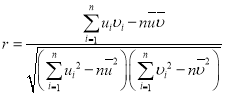 .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】在锐角△ABC中,a=2![]() ,_______,求△ABC的周长l的范围.
,_______,求△ABC的周长l的范围.
在①![]() (﹣cos
(﹣cos![]() ,sin
,sin![]() ),
),![]() (cos
(cos![]() ,sin
,sin![]() ),且
),且![]()
![]() ,②cosA(2b﹣c)=acosC,③f(x)=cosxcos(x
,②cosA(2b﹣c)=acosC,③f(x)=cosxcos(x![]() )
)![]() ,f(A)
,f(A)![]()
注:这三个条件中任选一个,补充在上面问题中并对其进行求解.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,椭圆![]() 的右顶点为
的右顶点为![]() ,左、右焦点分别为
,左、右焦点分别为![]() 、
、![]() ,过点
,过点![]()
且斜率为![]() 的直线与
的直线与![]() 轴交于点
轴交于点![]() , 与椭圆交于另一个点
, 与椭圆交于另一个点![]() ,且点
,且点![]() 在
在![]() 轴上的射影恰好为点
轴上的射影恰好为点![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)过点![]() 且斜率大于
且斜率大于![]() 的直线与椭圆交于
的直线与椭圆交于![]() 两点(
两点(![]() ),若
),若![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]()
![]() 的焦点为
的焦点为![]() ,点
,点![]() 为抛物线
为抛物线![]() 上一点,且点
上一点,且点![]() 到焦点
到焦点![]() 的距离为
的距离为![]() .
.
(1)求拋物线![]() 的标准方程;
的标准方程;
(2)设直线![]() 在
在![]() 轴上的截距为
轴上的截距为![]() ,且与抛物线交于
,且与抛物线交于![]() ,
,![]() 两点,连接
两点,连接![]() 并延长交抛物线的准线于点
并延长交抛物线的准线于点![]() ,当直线
,当直线![]() 恰与抛物线相切时,求直线
恰与抛物线相切时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】为阻隔新冠肺炎病毒,多地进行封城.封城一段时间后,有的人情绪波动不大,反应一般;也有的人情绪波动大,反应强烈.某社区为了解民众心理反应,随机调查了100位居民,得到数据如下表:
反应强烈 | 反应一般 | 合计 | |
男 | 20 | 20 | 40 |
女 | 45 | 15 | 60 |
合计 | 65 | 35 | 100 |
(1)以这100个人的样本数据估计该市的总体数据,且以频率估计概率,若从该社区的男性居民中随机抽取3位,记其中反应强烈的人数为X,求随机变量X的分布列和数学期望;
(2)根据调查数据,能否在犯错的概率不超过![]() 的前提下认为“反应强烈”与性别有关,并说明理由.
的前提下认为“反应强烈”与性别有关,并说明理由.
参考数据:
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
(参考公式: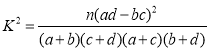 ,其中
,其中![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com