
科目: 来源: 题型:单选题
查看答案和解析>>
科目: 来源: 题型:单选题
查看答案和解析>>
科目: 来源: 题型:填空题
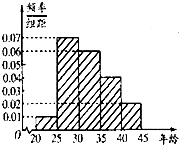 某市为增强市民的节约粮食意识,面向全市征召务宣传志愿者现从符合条件的志愿者中随机抽取100名按年龄分组:第1组[20,25),第2组[25,30),第3组[30,35),第4组[35,40),第5组[40,45],得到的频率分布直方图如图所示.若用分层抽样的方法从第3,4,5组中共抽取了12名志愿者参加l0月16日的“世界粮食日”宣传活动,则从第4组中抽取的人数为________.
某市为增强市民的节约粮食意识,面向全市征召务宣传志愿者现从符合条件的志愿者中随机抽取100名按年龄分组:第1组[20,25),第2组[25,30),第3组[30,35),第4组[35,40),第5组[40,45],得到的频率分布直方图如图所示.若用分层抽样的方法从第3,4,5组中共抽取了12名志愿者参加l0月16日的“世界粮食日”宣传活动,则从第4组中抽取的人数为________.查看答案和解析>>
科目: 来源: 题型:单选题
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
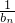 是等差数列,并求bn;
是等差数列,并求bn;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com