
分析 研究卫星绕行星做匀速圆周运动,根据万有引力提供向心力,列出等式求出中心体的质量.不考虑天体的自转,对任何天体表面都可以认为万有引力等于重力.
解答 解:(1)卫星绕行星做匀速圆周运动,轨道半径(R+h),根据万有引力提供向心力有:
$G\frac{mm′}{(R+h)_{\;}^{2}}=m′\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}(R+h)$
解:$m=\frac{4{π}_{\;}^{2}(R+h)_{\;}^{3}}{G{T}_{\;}^{2}}$
(2)根据$ρ=\frac{m}{V}=\frac{\frac{4{π}_{\;}^{2}(R+h)_{\;}^{3}}{G{T}_{\;}^{2}}}{\frac{4}{3}π{R}_{\;}^{3}}$=$\frac{3π(R+h)_{\;}^{3}}{G{T}_{\;}^{2}{R}_{\;}^{3}}$
(3)根据重力等于万有引力得$m′g=G\frac{mm′}{{R}_{\;}^{2}}$
得$g=\frac{Gm}{{R}_{\;}^{2}}=\frac{4{π}_{\;}^{2}(R+h)_{\;}^{3}}{{T}_{\;}^{2}{R}_{\;}^{2}}$
答:(1)行星的质量$\frac{4{π}_{\;}^{2}(R+h)_{\;}^{3}}{G{T}_{\;}^{2}}$
(2)行星的平均密度$\frac{3π(r+h)_{\;}^{3}}{G{T}_{\;}^{2}{R}_{\;}^{3}}$
(3)行星表面的重力加速度是$\frac{4{π}_{\;}^{2}(R+h)_{\;}^{3}}{{T}_{\;}^{2}{R}_{\;}^{2}}$
点评 本题考查了万有引力在天体中的应用,解题的关键在于找出向心力的来源,并能列出等式解题.向心力的公式选取要根据题目提供的已知物理量或所求解的物理量选取应用.


 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中物理 来源: 题型:选择题
| A. | 洛伦兹力始终与速度v垂直 | B. | 洛伦兹力的方向与速度无关 | ||
| C. | 洛伦兹力的大小与速度无关 | D. | 洛伦兹力不改变带电粒子的速度 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
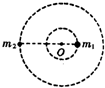 经长期观测人们在宇宙中已经发现了“双星系统”,“双星系统”由两颗相距较近的恒星组成,每个恒星的线度远小于两个星体之间的距离,而且双星系统一般远离其他天体.如图所示,两颗星球组成的双星,在相互之间的万有引力作用下,绕连线上的O点做周期相同的匀速圆周运动.现测得两颗星之间的距离为L,质量之比为m1:m2=5:2.则可知( )
经长期观测人们在宇宙中已经发现了“双星系统”,“双星系统”由两颗相距较近的恒星组成,每个恒星的线度远小于两个星体之间的距离,而且双星系统一般远离其他天体.如图所示,两颗星球组成的双星,在相互之间的万有引力作用下,绕连线上的O点做周期相同的匀速圆周运动.现测得两颗星之间的距离为L,质量之比为m1:m2=5:2.则可知( )| A. | m1、m2做圆周运动的线速度之比为2:5 | |
| B. | m1、m2做圆周运动的角速度之比为5:2 | |
| C. | m1做圆周运动的半径为$\frac{2}{7}L$ | |
| D. | m2做圆周运动的半径为$\frac{2}{7}L$ |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 天体A、B的密度不同 | |
| B. | 天体A、B的质量一定相等 | |
| C. | 两颗卫星的线速度一定相等 | |
| D. | 天体A、B表面的重力加速度与它们的半径成正比 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,一个轻杆倾斜放置,杆上固定两个质量相同的小球A和B,绕竖直轴线转动,A和B分别在图示所在的水平面内做匀速圆周运动,则( )
如图所示,一个轻杆倾斜放置,杆上固定两个质量相同的小球A和B,绕竖直轴线转动,A和B分别在图示所在的水平面内做匀速圆周运动,则( )| A. | A球线速度必定等于B球的线速度 | |
| B. | A球对筒壁的压力必定大于B球对筒壁的压力 | |
| C. | A球角速度必定大于B球的角速度 | |
| D. | A球的运动周期必定大于B球的运动周期 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com