
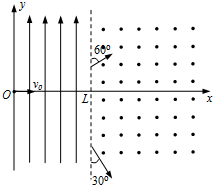
 ��ͼ��ʾ����xOyƽ����0��x��L����������һ������ֱ���ϵ���ǿ�糡��x��L����������һ����ֱ��xOyƽ���������ǿ�ų���ijʱ�̣�һ����������Ӵ�����ԭ�㣬����x��������ij��ٶ�v0����糡��֮�����һʱ�̣�һ������������ͬ���ij��ٶȴ�����ԭ�����糡�����������Ӵӵ糡����ų�ʱ�ٶȷ�����糡�ʹų��߽�ļнǷֱ�Ϊ60���30�㣬�������ڴų��зֱ��˶����ܺ�ǡ����ij����������֪�����ӵ������Լ�������֮�������ö��ɺ��Բ��ƣ���
��ͼ��ʾ����xOyƽ����0��x��L����������һ������ֱ���ϵ���ǿ�糡��x��L����������һ����ֱ��xOyƽ���������ǿ�ų���ijʱ�̣�һ����������Ӵ�����ԭ�㣬����x��������ij��ٶ�v0����糡��֮�����һʱ�̣�һ������������ͬ���ij��ٶȴ�����ԭ�����糡�����������Ӵӵ糡����ų�ʱ�ٶȷ�����糡�ʹų��߽�ļнǷֱ�Ϊ60���30�㣬�������ڴų��зֱ��˶����ܺ�ǡ����ij����������֪�����ӵ������Լ�������֮�������ö��ɺ��Բ��ƣ������� ��1�������ڵ糡������ƽ���˶������˶��ֽ⣬���ţ�ٵڶ����ɼ��������
��2�������ڴų���������Բ���˶������������ṩ����������ţ�ٵڶ����ɼ���������ǵİ뾶��
��3����������뾶�Ĺ�ϵ��$T=\frac{2��r}{v}$�ֱ�������ǵ����ڣ�Ȼ��������ǵĴų����˶� ��ʱ�䣬��������������Ⱥ����糡��ʱ��
��� 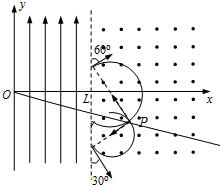 �⣺��1�������ӽ��ų�������߽�н�Ϊ�ȣ�������ˮƽ����������ֱ���˶�����
�⣺��1�������ӽ��ų�������߽�н�Ϊ�ȣ�������ˮƽ����������ֱ���˶�����
$t=\frac{L}{{v}_{0}}$
�ص糡�ߵķ���$a=\frac{qE}{m}$��vy=at
�֣�$tan��=\frac{{v}_{y}}{{v}_{0}}$=$\frac{qEL}{m{v}_{0}^{2}}$
�����ã�
$\frac{{q}_{1}}{{m}_{1}}��\frac{{q}_{2}}{{m}_{2}}=\frac{1}{tan60��}��\frac{1}{tan30��}=1��3$
��2�������ڵ糡�е�ƫת����$y=\frac{1}{2}a{t}^{2}=\frac{qE{L}^{2}}{2m{v}_{0}^{2}}$��$\frac{q}{m}$
���ԣ�$\frac{{y}_{1}}{{y}_{2}}=\frac{1}{3}$
�֣�$y=\frac{{v}_{y}}{2}t$
�������뿪�糡λ�ü�ľ��룺d=y1+y2
�ų���Բ���˶��ٶȣ�$v=\frac{{v}_{0}}{sin��}$��
���ԣ�${v}_{1}=\frac{{v}_{0}}{sin60��}=\frac{2\sqrt{3}}{3}{v}_{0}$��${v}_{2}=\frac{{v}_{0}}{sin30��}=2{v}_{0}$
�����������ṩ�������ã�$qvB=\frac{m{v}^{2}}{r}$��
�ã�$r=\frac{mv}{qB}$��
���ԣ�$\frac{{r}_{1}}{{r}_{2}}=\frac{\sqrt{3}}{1}$
�������������˶��켣��������������P�㣬
�ɼ��ι�ϵ�ɵã�
2r1=dsin60��
2r2=dsin30��
������ã�${r}_{1}=\frac{\sqrt{3}d}{4}=\frac{1}{2}L$��${r}_{2}=\frac{1}{4}d=\frac{\sqrt{3}}{6}L$
��3�������ڴų����˶������ڣ�$T=\frac{2��r}{v}$
�������ڴų����˶�ʱ���Ϊ������ڣ���t1=$\frac{��{r}_{1}}{{v}_{1}}=\frac{��•\frac{1}{2}L}{\frac{2\sqrt{3}}{3}{v}_{0}}=\frac{\sqrt{3}��L}{4{v}_{0}}$��${t}_{2}=\frac{��{r}_{2}}{{v}_{2}}=\frac{��•\frac{\sqrt{3}}{6}L}{2{v}_{0}}=\frac{\sqrt{3}��L}{12{v}_{0}}$
�����������ڵ糡��ʱ����ͬ�����Խ��糡ʱ��Ϊ�ų�������ǰ��ʱ��
$��t={t}_{1}-{t}_{2}=\frac{\sqrt{3}��L}{4{v}_{0}}-\frac{\sqrt{3}��L}{12{v}_{0}}=\frac{\sqrt{3}��L}{6{v}_{0}}$
�𣺣�1�����������ӵıȺ�֮����1��3��
��2�������������ڴų����˶��İ뾶��С�ֱ���$\frac{1}{2}L$��$\frac{\sqrt{3}}{6}L$��
��3���������Ⱥ����糡��ʱ�����$\frac{\sqrt{3}��L}{6{v}_{0}}$��
���� ���⿼����������ڵ糡�е��˶��ʹ��������ڴų��е��˶���������븺�����Ȼƫת�ķ����෴�������˶��Ĺ��ɻ�����ͬ�����������ͨʽ�پ���ֿ���Ҳ����ֱ�ӷֱ�����������Լ���ϰ������𣬴�Ծͺã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ���ļ��ٶ���������Բ���˶����������ٶȷ���仯������������ | |
| B�� | ������������Բ���˶��������ܵĺ����� | |
| C�� | ����Բ���˶����ȱ��������˶� | |
| D�� | ��Ϊ���ٶȷ���ʱ�̱仯����������Բ���˶����������˶� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
| ʱ��t/s | 0 | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 |
| �ٶ�v/��ms-1�� | 0 | 0.16 | 0.31 | 0.45 | 0.52 | 0.58 | 0.60 |

�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ��ʾ��һ�ι��ά�ļ�ͼ�������ܳ�ΪL����֪��������������ڹ��˵IJ�����ǡ���ܷ���ȫ���䣮����֪�ù��˵�������Ϊn����������д����ٶ�Ϊc����
��ͼ��ʾ��һ�ι��ά�ļ�ͼ�������ܳ�ΪL����֪��������������ڹ��˵IJ�����ǡ���ܷ���ȫ���䣮����֪�ù��˵�������Ϊn����������д����ٶ�Ϊc�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 һ�м�г�Შ��x����������t=0ʱ�̲�����ͼ��ʾ����ʱ�̺�����е�P�ʵ�ص�ƽ��λ�õ����ʱ��Ϊ0.2s��Q�ʵ�ص�ƽ��λ�õ����ʱ��Ϊ1s����֪t=0ʱ��P��Q���ʵ��ƽ��λ�õ�λ����ͬ��������
һ�м�г�Შ��x����������t=0ʱ�̲�����ͼ��ʾ����ʱ�̺�����е�P�ʵ�ص�ƽ��λ�õ����ʱ��Ϊ0.2s��Q�ʵ�ص�ƽ��λ�õ����ʱ��Ϊ1s����֪t=0ʱ��P��Q���ʵ��ƽ��λ�õ�λ����ͬ��������| A�� | �ü�г��������Ϊ1.2s | B�� | �ü�г���IJ���Ϊ0.05m/s | ||
| C�� | t=0.8sʱ��P�ʵ�ļ��ٶ�Ϊ�� | D�� | ����1s���ʵ�Q�����ƶ���1m |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ��LOO��L��Ϊһ���ߣ������γɵ������ǡ�LOO��͡�OO��L���Ϊ45�㣮���ߵ��ұ���һ��ǿ�ų����䷽��ֱ��ֽ�����һ�߳�Ϊl�������ε��߿��ش�ֱ��OO��ķ������ٶ�v����ֱ���ϵ�����ֱ���˶�����t=0ʱ��ǡ��λ��ͼ����ʾλ�ã�����ʱ�뷽��Ϊ���߿��е������������������ķ�ͼ���ܹ���ȷ��ʾ����-ʱ�䣨I-t����ϵ���ǣ�ʱ����$\frac{l}{v}$Ϊ��λ����������
��ͼ��ʾ��LOO��L��Ϊһ���ߣ������γɵ������ǡ�LOO��͡�OO��L���Ϊ45�㣮���ߵ��ұ���һ��ǿ�ų����䷽��ֱ��ֽ�����һ�߳�Ϊl�������ε��߿��ش�ֱ��OO��ķ������ٶ�v����ֱ���ϵ�����ֱ���˶�����t=0ʱ��ǡ��λ��ͼ����ʾλ�ã�����ʱ�뷽��Ϊ���߿��е������������������ķ�ͼ���ܹ���ȷ��ʾ����-ʱ�䣨I-t����ϵ���ǣ�ʱ����$\frac{l}{v}$Ϊ��λ����������| A�� | 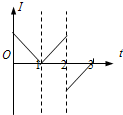 | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ���о�ƽ���˶���ʵ���У���С���δ�б���Ϲ��£��ڰ�ֽ�����μ���С���λ�ã�ij��ij�ҵõ��ļ�¼ֽ�ֱ���ͼ��ʾ����ͼ�����Կ���
���о�ƽ���˶���ʵ���У���С���δ�б���Ϲ��£��ڰ�ֽ�����μ���С���λ�ã�ij��ij�ҵõ��ļ�¼ֽ�ֱ���ͼ��ʾ����ͼ�����Կ����鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com