
 ��ͼ��ʾ����S��ĵ����Ϊq������Ϊm�ľ�ֹ�������ӣ������ٵ�ѹΪU����������Ϊd����ǿ�糡���ٺ������봹ֱ�����ѹΪU����ǿƫת�糡��ƫת���峤�Ⱥͼ�������ΪL������������Ӱ�죩
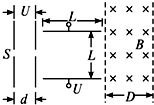
��ͼ��ʾ����S��ĵ����Ϊq������Ϊm�ľ�ֹ�������ӣ������ٵ�ѹΪU����������Ϊd����ǿ�糡���ٺ������봹ֱ�����ѹΪU����ǿƫת�糡��ƫת���峤�Ⱥͼ�������ΪL������������Ӱ�죩���� ��1�����ڼ��ٵ糡�����ö��ܶ����������ƫת�糡������ƽ���˶����ƫתλ�ƵĴ�С��ƫת�ǣ�
��2���������������ö��ܶ�����������ӽ���ų����ٶȣ���ϰ뾶��ʽ��������ڴų����˶��İ뾶����ϼ��ι�ϵ�����ǿ�ų�����С���ȣ������ڼ��ٵ糡���ȼ���ֱ���ȼ���ֱ���˶�����ƫת�糡������ƽ���˶����ڴų���������Բ���˶�������˶�ѧ��ʽ�������Լ��ڴų����˶������ڹ�ʽ����������ӵ�����T��ƫת��ѹ�������任һ�η����ʱ����������ڴų����˶���ʱ�䣮
���  �⣺��1����ֱ���ٹ��̣����ݶ��ܶ������У�
�⣺��1����ֱ���ٹ��̣����ݶ��ܶ������У�
qU=$\frac{1}{2}m{v}^{2}$
�ʼ��ٺ������ٶȣ�
v0=$\sqrt{\frac{2Uq}{m}}$
��ƫת�糡��������ƽ���˶����ʣ�
L=v0t
y=$\frac{1}{2}a{t}^{2}$
����
a=$\frac{qU}{md}$
���ڼ����з���ʱ�䣺
t=$\frac{L}{{v}_{0}}$
�ڼ�������һ��ֱ�ڳ��ٶȷ������������t��ֱ�����λ��Ϊ��
y=$\frac{1}{2}$$\frac{Uq}{mL}$t2=$\frac{L}{4}$
��ֱ���ٶ�Ϊ��
vy=$\frac{Uq}{mL}$t=$\sqrt{\frac{Uq}{2m}}$
�ٶ�ƫת�����У�
$tan��=\frac{{v}_{y}}{{v}_{x}}$=$\frac{\sqrt{\frac{Uq}{2m}}}{\sqrt{\frac{2Uq}{m}}}$=$\frac{1}{2}$
��ƫ�ƾ���$\frac{L}{4}$��ƫת�Ƕ�arctan$\frac{1}{2}$��
��2�����ӵ��˶��켣�ǶԳƵģ��ڴų��еIJ�����һ���Ż������İ뾶$R=\frac{mv}{qB}=\frac{m}{qB}\sqrt{\frac{5qU}{2m}}$����߽�������ٶȷ������У���ų����ȣ�
D=R$\frac{5+\sqrt{5}}{5}$=��5+$\sqrt{5}$��$\sqrt{\frac{qU}{10m}}$��
ͨ���û���ʱ$\frac{2��m}{qB}����-arctan2��$����ƫת�����������L$\sqrt{\frac{2m}{qU}}$�����ټ����������2d$\sqrt{\frac{2m}{qU}}$����
T=$\frac{2��}{qB}����-arctan2��+L\sqrt{\frac{2m}{qU}}+2d\sqrt{\frac{2m}{qU}}$��ƫת�糡����ÿ��$\frac{T}{2}$�ı伴�ɣ�
�𣺣�1�����������뿪ƫת�糡ʱ�ش�ֱ�ڰ��淽��ƫ�Ƶľ���Ϊ$\frac{L}{4}$��ƫת�ĽǶ�Ϊarctan$\frac{1}{2}$��
��2����ǿ�ų��Ŀ���D����Ϊ��5+$\sqrt{5}$��$\sqrt{\frac{qU}{10m}}$���ô��������������˶�������T��$\frac{2��}{qB}����-arctan2��+L\sqrt{\frac{2m}{qU}}+2d\sqrt{\frac{2m}{qU}}$��ƫת��ѹ������ʱ��ÿ��$\frac{T}{2}$�任һ�η���
���� ���⿼���������ڵ糡�кʹų��е��˶����⣬�ؼ��������ӵĹ켣��֪�������ڼ��ٵ糡�����ȼ���ֱ���˶�����ƫת�糡������ƽ���˶�������ǿ�ų�����Բ���˶�����϶��ܶ������˶�ѧ��ʽ������⣮


 ��������ϵ�д�
��������ϵ�д� ����˼ά����ѵ����ʱ��ѧ��ϵ�д�
����˼ά����ѵ����ʱ��ѧ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ������
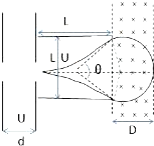
 ��ͼ��ʾ����ֱ���õ�ƽ�н����壬����ѹΪU0������Ϊm������Ϊq�Ĵ���������ӣ����������������a���ɾ�ֹ�ͷţ����ٺ���Ҽ����С��b�������o�㴹ֱ��mf�ߵķ�������߳�ΪL�������γ�����oΪmf�ߵ��е㣮
��ͼ��ʾ����ֱ���õ�ƽ�н����壬����ѹΪU0������Ϊm������Ϊq�Ĵ���������ӣ����������������a���ɾ�ֹ�ͷţ����ٺ���Ҽ����С��b�������o�㴹ֱ��mf�ߵķ�������߳�ΪL�������γ�����oΪmf�ߵ��е㣮�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
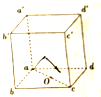 ��ͼ��ʾ������ǿ�糡����һ�����壬�糡�ߵķ�����ֱ��a��dƽ�У�a���ĵ��Ʀ�1=2V��d��ĵ��Ʀ�2=-2V��O����a��c���ߵ��е㣮��֪Ԫ��ɵ����e=1.6��10-19 J��������˵����ȷ���ǣ�������
��ͼ��ʾ������ǿ�糡����һ�����壬�糡�ߵķ�����ֱ��a��dƽ�У�a���ĵ��Ʀ�1=2V��d��ĵ��Ʀ�2=-2V��O����a��c���ߵ��е㣮��֪Ԫ��ɵ����e=1.6��10-19 J��������˵����ȷ���ǣ�������| A�� | ����һ�����Ӵ�O���Ƶ�a�㣬�糡������1.6��10-19J | |
| B�� | ����һ�����Ӵ�O���Ƶ�a�㣬�糡������3.2��10-19J | |
| C�� | ����һ�����Ӵ�O���Ƶ�c�㣬�糡������-1.6��10-19J | |
| D�� | ����һ�����Ӵ�O���Ƶ�c�㣬�糡������-3.2��10-19J |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 һ����Ϊ1kg������Ӹ�h=5m�Ĺ⻬б�涥�˾�ֹ�ͷţ����䵽б��ˣ���
һ����Ϊ1kg������Ӹ�h=5m�Ĺ⻬б�涥�˾�ֹ�ͷţ����䵽б��ˣ����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
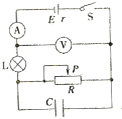
| A�� | ������������С����ѹ��������� | B�� | ��Դ���ܹ��ʱ�� | ||
| C�� | ������C�ϵ������С | D�� | С����L�䰵 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
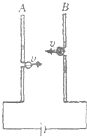 ��ͼ��ʾ��ƽ�н�����A��B���е�����ŵ�ɣ����Ӻ����Ӿ�������v�ֱ������A�壩������B�壩�������ϵ�С���ش�ֱ����ķ��������䣬��ô��������
��ͼ��ʾ��ƽ�н�����A��B���е�����ŵ�ɣ����Ӻ����Ӿ�������v�ֱ������A�壩������B�壩�������ϵ�С���ش�ֱ����ķ��������䣬��ô��������| A�� | �������ܵ���A�壬�����Ҳһ���ܵ���B�� | |
| B�� | �������ܵ���B�壬������Ҳһ���ܵ���A�� | |
| C�� | �����ӡ����Ӿ��ֱ��ܵ���A��B�壬����ӡ������ڰ���˶��Ĺ����еĶ��ܸı�������� | |
| D�� | �����ӡ����Ӿ��ֱ��ܵ���A��B�壬����ӡ������ڰ���˶��Ĺ����еĶ��ܸı������ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
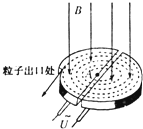 ����˹������˹��ƵĻ�������������ԭ����ͼ��ʾ�����ڸ�����е�D�ν����뾶ΪR�����м�������С���������Ӵ�����ʱ��ɺ��ԣ��Ÿ�Ӧǿ��ΪB����ǿ�ų�����洹ֱ����Ƶ������Ƶ��Ϊf�����ٵ�ѹΪU����A������Դ��������������Ϊm�������Ϊ+q���ڼ������б����٣��Ҽ��ٹ����в����������ЧӦ��������Ӱ�죬������˵����ȷ���ǣ�������
����˹������˹��ƵĻ�������������ԭ����ͼ��ʾ�����ڸ�����е�D�ν����뾶ΪR�����м�������С���������Ӵ�����ʱ��ɺ��ԣ��Ÿ�Ӧǿ��ΪB����ǿ�ų�����洹ֱ����Ƶ������Ƶ��Ϊf�����ٵ�ѹΪU����A������Դ��������������Ϊm�������Ϊ+q���ڼ������б����٣��Ҽ��ٹ����в����������ЧӦ��������Ӱ�죬������˵����ȷ���ǣ�������| A�� | ���ӱ����ٺ������ٶȲ����ܳ���2��Rf | |
| B�� | �����뿪����������ʱ�����������ٵ�ѹU������ | |
| C�� | �����뿪����������ʱ��������뽻����Ƶ��f������ | |
| D�� | ���ӵ�2�κ͵�1�ξ�����D�κм���������뾶֮��Ϊ$\sqrt{2}$��1 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 ��ͼΪ���µ緹���ĵ�·ͼ��R1��R2Ϊ����˿��SΪ�¿ؿ��أ����ڼ�ͥ��·�ϣ�R1��R2=9��1������ʱ�Ĺ���Ϊ1000W��������
��ͼΪ���µ緹���ĵ�·ͼ��R1��R2Ϊ����˿��SΪ�¿ؿ��أ����ڼ�ͥ��·�ϣ�R1��R2=9��1������ʱ�Ĺ���Ϊ1000W��������| A�� | S�Ͽ�ʱ���緹�����ڼ���״̬ | |
| B�� | S�պ�ʱ���緹�����ڼ���״̬ | |
| C�� | ����״̬ʱ��Դ���������Ϊ100W | |
| D�� | ����״̬ʱ��Դ���������Ϊ$\frac{1000}{9}$w |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 ��ͼ��ʾ����ֱ���õ�����ƽ�н�������֮����ж�ֵ����R���������ܺ��ԵĽ�������������ʼ�ձ��ִ�ֱ�����ýӴ�����Ħ�������뵼��ĵ�������ƣ�����װ�÷�����ǿ�ų��У��ų������뵼��ƽ�洹ֱ��������ֱ���ϵĺ���F�����¼���������һ��ʱ���ڣ���F���Ĺ��밲�������Ĺ��Ĵ����ͣ�������
��ͼ��ʾ����ֱ���õ�����ƽ�н�������֮����ж�ֵ����R���������ܺ��ԵĽ�������������ʼ�ձ��ִ�ֱ�����ýӴ�����Ħ�������뵼��ĵ�������ƣ�����װ�÷�����ǿ�ų��У��ų������뵼��ƽ�洹ֱ��������ֱ���ϵĺ���F�����¼���������һ��ʱ���ڣ���F���Ĺ��밲�������Ĺ��Ĵ����ͣ�������| A�� | ���ڰ��Ļ�е�������� | B�� | ���ڰ��Ķ��������� | ||
| C�� | ���ڰ����������������� | D�� | ���ڵ���R�Ϸų������� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com