
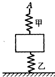
 如图所示,物块质量为m,与甲、乙两弹簧相连接,乙弹簧下端与地面连接,甲、乙两弹簧质量不计,其劲度系数分别为k1、k2,起初甲弹簧处于自由长度,现用手将甲弹簧的A端缓慢上提,使乙弹簧产生的弹力大小变为原来的$\frac{2}{3}$,则A端上移距离可能是( )
如图所示,物块质量为m,与甲、乙两弹簧相连接,乙弹簧下端与地面连接,甲、乙两弹簧质量不计,其劲度系数分别为k1、k2,起初甲弹簧处于自由长度,现用手将甲弹簧的A端缓慢上提,使乙弹簧产生的弹力大小变为原来的$\frac{2}{3}$,则A端上移距离可能是( )| A. | $\frac{{(k}_{1}{+k}_{2})mg}{{{3k}_{1}k}_{2}}$ | B. | $\frac{2{(k}_{1}{+k}_{2})mg}{{{3k}_{1}k}_{2}}$ | ||
| C. | $\frac{4{(k}_{1}{+k}_{2})mg}{{{3k}_{1}k}_{2}}$ | D. | $\frac{5{(k}_{1}{+k}_{2})mg}{{{3k}_{1}k}_{2}}$ |
分析 题中要求弹簧乙产生的弹力大小变成原来的$\frac{2}{3}$,此时乙弹簧有两种可能的状态:拉伸和压缩.乙原来处于压缩状态,后来处于拉伸或压缩状态,根据胡克定律分别求出B原来压缩量和后来的伸长量或压缩量,即可得到M上移的距离.再根据胡克定律求出甲的伸长量,加上M上移的距离就是A端上移的距离.
解答 解:乙弹簧原先处于压缩状态,压缩量为:x1=$\frac{mg}{{k}_{2}}$,甲弹簧无形变.
情况一:用手拉住弹簧A的上端,缓慢上移时,B弹簧仍处于压缩状态,压缩量:
x2=$\frac{2mg}{3{k}_{2}}$
则物体m上升的距离为:
S1=x1-x2=$\frac{mg}{{k}_{2}}-\frac{2mg}{{3k}_{2}}=\frac{mg}{3{k}_{2}}$
由m受力平衡可知,甲弹簧处于拉伸状态,伸长量:
x3=$\frac{mg}{3{k}_{1}}$
则A的上端应上移为:l1=S1+x3=$\frac{mg}{3{k}_{2}}+\frac{mg}{3{k}_{1}}$=$\frac{mg({k}_{1}+{k}_{2})}{3{k}_{1}{k}_{2}}$;
情况二:用手拉住弹簧A的上端,缓慢上移时,B弹簧处于拉伸状态,伸长量:
x2=$\frac{2mg}{3{k}_{2}}$;
则物体m上升的距离为:
S2=x1+x2=$\frac{mg}{{k}_{2}}+\frac{2mg}{{3k}_{2}}=\frac{5mg}{3{k}_{2}}$
由m受力平衡可知,A弹簧处于拉伸状态,形变量:
x4=$\frac{5mg}{3{k}_{1}}$
则A的上端应上移:
l2=S2+x4=$\frac{5mg}{3{k}_{1}}+\frac{5mg}{3{k}_{2}}$=$\frac{5mg({k}_{1}+{k}_{2})}{3{k}_{1}{k}_{2}}$
所以选项AD正确,BC错误
故选:AD
点评 本题的解题关键是分析弹簧的状态,分析出A端上移的距离与弹簧形变量的关系,要注意不能漏解.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案科目:高中物理 来源: 题型:计算题
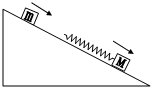 质量m和M的两木块分别以v1和v2的速度沿粗糙足够长的斜面匀速下滑.已知斜面固定,v1>v2.求两木块发生相互作用的过程中.轻质弹簧能达到的最大弹性势能.
质量m和M的两木块分别以v1和v2的速度沿粗糙足够长的斜面匀速下滑.已知斜面固定,v1>v2.求两木块发生相互作用的过程中.轻质弹簧能达到的最大弹性势能.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 物体速度不为零,其加速度也一定不为零 | |
| B. | 物体加速度方向改变时,速度方向可以保持不变 | |
| C. | 物体具有加速度时,它的速度可能不会改变 | |
| D. | 物体的加速度变大时,速度也一定随之变大 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
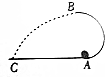 如图所示,半径为R的半圆形轨道竖直固定在水平地面上,A点是最低点,B点是最高点,质量为m的小球以5$\sqrt{gR}$的速度自A点进入半圆轨道,它经过最高点后飞出,最后落在水平地面上的C点,现测得AC=4R,重力加速度为g,不计空气阻力.求:
如图所示,半径为R的半圆形轨道竖直固定在水平地面上,A点是最低点,B点是最高点,质量为m的小球以5$\sqrt{gR}$的速度自A点进入半圆轨道,它经过最高点后飞出,最后落在水平地面上的C点,现测得AC=4R,重力加速度为g,不计空气阻力.求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
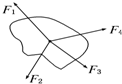 如图所示,某物体在四个共点力作用下处于平衡状态,若将F4=5N的力沿逆时针方向转动90°,其余三个力的大小和方向不变,则此时物体所受合力的大小为( )
如图所示,某物体在四个共点力作用下处于平衡状态,若将F4=5N的力沿逆时针方向转动90°,其余三个力的大小和方向不变,则此时物体所受合力的大小为( )| A. | 0 | B. | 10 N | C. | 5$\sqrt{2}$ N | D. | $\frac{5\sqrt{2}}{2}$ N |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,粗糙的固定斜面上放置一质量为m的木箱,斜面的倾角为α=30°,木箱与斜面间的动摩擦因数为μ=$\frac{{\sqrt{3}}}{3}$,先对木箱施一拉力F,使木箱沿斜面向上做匀速直线运动.设F的方向与水平面的夹角为θ(图中未画出),在θ从0°逆时针逐渐增大到90°的过程中,木箱的速度保持不变,则( )
如图所示,粗糙的固定斜面上放置一质量为m的木箱,斜面的倾角为α=30°,木箱与斜面间的动摩擦因数为μ=$\frac{{\sqrt{3}}}{3}$,先对木箱施一拉力F,使木箱沿斜面向上做匀速直线运动.设F的方向与水平面的夹角为θ(图中未画出),在θ从0°逆时针逐渐增大到90°的过程中,木箱的速度保持不变,则( )| A. | F一直减小 | |
| B. | F的最小值为$\frac{{\sqrt{3}}}{2}$mg | |
| C. | F先减小后增大 | |
| D. | 当θ=0°时,斜面对m的作用力为Fsina+mgcosa |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
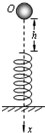 如图所示,劲度系数为k的轻弹簧竖直放置,下端固定在水平地面上,一质量为m的小球,从离弹簧上端高h处由静止释放,那么从小球压上弹簧后继续向下运动到最低点的过程中,以下说法正确的是( )
如图所示,劲度系数为k的轻弹簧竖直放置,下端固定在水平地面上,一质量为m的小球,从离弹簧上端高h处由静止释放,那么从小球压上弹簧后继续向下运动到最低点的过程中,以下说法正确的是( )| A. | 弹簧的弹性势能逐渐增大 | |
| B. | 球刚接触弹簧时动能最大 | |
| C. | 全过程中小球的机械能守恒 | |
| D. | 该过程的某一阶段内,小球的动能增大而小球的机械能减少 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 氢原子巴尔末系谱线是包含从红外到紫外的线状谱 | |
| B. | 氢气放电管内气体导电发光是热辐射现象 | |
| C. | 氢原子光谱的不连续性,表明氢原子的能级是不连续的 | |
| D. | 根据各种原子发光的特征谱线进行光谱分析,可以鉴别物质和确定物质的成分 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com