
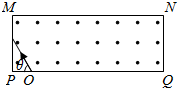
 如图所示,在矩形PQNM中有垂直纸面向外的匀强磁场,PQ和PM的长度分别为8L和3L,O为pQ上一点,OP长度为L.一个带正电荷的粒子从O点以速度v0射入磁场中,粒子质量为m,带电荷量为e.
如图所示,在矩形PQNM中有垂直纸面向外的匀强磁场,PQ和PM的长度分别为8L和3L,O为pQ上一点,OP长度为L.一个带正电荷的粒子从O点以速度v0射入磁场中,粒子质量为m,带电荷量为e.分析 粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,作出粒子运动轨迹,求出粒子轨道半径,然后由牛顿第二定律求出磁感应强度的最小值;根据粒子做圆周运动的周期公式与粒子在磁场中转过的圆心角可以求出粒子在磁场中的运动时间.
解答 解:(1)粒子速度垂直PQ向上,粒子恰好从PQ边射出,轨道半径最大时的运动轨迹如图所示,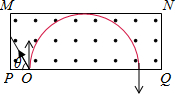
由几何知识得,粒子轨道半径:r=3L,
粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,
由牛顿第二定律得:ev0B1=m$\frac{{v}_{0}^{2}}{r}$,解得:B1=$\frac{m{v}_{0}}{3eL}$,
粒子在磁场中的运动时间:t=$\frac{θ}{360°}$T=$\frac{180°}{360°}$×$\frac{2πm}{e{B}_{1}}$=$\frac{3πL}{{v}_{0}}$;
(2)粒子速度与QP成夹角θ=60℃向上,粒子恰好从PQ边射出,轨道半径最大时的运动轨迹如图所示,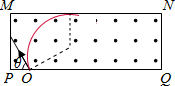
由几何知识得,粒子轨道半径:r′+r′sin30°=3L,r′=2L,
粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,
由牛顿第二定律得:ev0B2=m$\frac{{v}_{0}^{2}}{r′}$,解得:B2=$\frac{m{v}_{0}}{2eL}$,
粒子在磁场中的运动时间:t′=$\frac{θ′}{360°}$T′=$\frac{180°-60°}{360°}$×$\frac{2πm}{e{B}_{2}}$=$\frac{4πL}{3{v}_{0}}$;
答:(1)若带电荷粒子速度垂直PQ向上,欲使粒子从PQ离开磁场,求磁感应强度的最小值B1为$\frac{m{v}_{0}}{3eL}$,粒子在磁场中的运动时间为$\frac{3πL}{{v}_{0}}$;
(2)若此带电粒子速度与QP成夹角θ=60℃向上,欲使此粒子从PQ离开磁场,磁感应强度的最小值B2为$\frac{m{v}_{0}}{2eL}$,粒子在磁场中的运动时间为$\frac{4πL}{3{v}_{0}}$.
点评 本题考查了粒子在磁场中的运动,考查了求磁感应强度与粒子的运动时间,分析清楚粒子运动过程、作出粒子运动轨迹是解题的关键,应用牛顿第二定律与粒子做圆周运动的周期公式可以解题.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:高中物理 来源: 题型:选择题
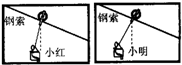 在一种速降娱乐项目中,人乘坐在吊篮中,吊篮通过滑轮沿一条倾斜的钢索向下滑行.现有两条彼此平行的钢索,小红和小明分别乘吊篮从速降的起点由静止开始下滑,在他们下滑过程中,当吊篮与滑轮达到相对静止状态时,分别拍下一张照片,如图所示.已知二人运动过程中,空气阻力的影响可以忽略.当吊篮与滑轮达到相对静止状态后,则( )
在一种速降娱乐项目中,人乘坐在吊篮中,吊篮通过滑轮沿一条倾斜的钢索向下滑行.现有两条彼此平行的钢索,小红和小明分别乘吊篮从速降的起点由静止开始下滑,在他们下滑过程中,当吊篮与滑轮达到相对静止状态时,分别拍下一张照片,如图所示.已知二人运动过程中,空气阻力的影响可以忽略.当吊篮与滑轮达到相对静止状态后,则( )| A. | 两人的运动都一定是匀速运动 | B. | 吊篮对小明的作用力向上 | ||
| C. | 小明的加速度大 | D. | 小明的合外力小 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,一个质量为m小球被夹在竖直的墙壁和A点之间且A到竖直墙的间距为d(且R<d<2R),已知球的半径为R,所有接触点和面均不计摩擦.试求小球对A点压力F1和竖直墙对球的弹力F2.(sin2θ+cos2θ=1)
如图所示,一个质量为m小球被夹在竖直的墙壁和A点之间且A到竖直墙的间距为d(且R<d<2R),已知球的半径为R,所有接触点和面均不计摩擦.试求小球对A点压力F1和竖直墙对球的弹力F2.(sin2θ+cos2θ=1)查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 导体A和导体B都带正电,且导体A的质子变多了 | |
| B. | 导体A和导体B都带正电,且导体A的负电荷变多了 | |
| C. | 导体A和导体B都带负电,且导体B的质子变多了 | |
| D. | 导体A和导体B都带负电,且导体B的负电荷变多了 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,一小球用轻质线悬挂在木板的支架上,木板沿倾角为θ的斜面下滑时,细线呈竖直状态,则在木板下滑的过程中,下列说法中正确的是( )
如图所示,一小球用轻质线悬挂在木板的支架上,木板沿倾角为θ的斜面下滑时,细线呈竖直状态,则在木板下滑的过程中,下列说法中正确的是( )| A. | 小球的机械能守恒 | |
| B. | 木板、小球组成的系统机械能守恒 | |
| C. | 木板与斜面间的动摩擦因数为$\frac{1}{tanθ}$ | |
| D. | 木板、小球组成的系统减少的机械能转化为内能 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
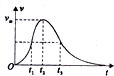 一滑块静止在光滑的水平地面上,某时刻开始,受到的水平力F作用后,速度v随时间t变化关系如图所示,则下列说法正确的是( )
一滑块静止在光滑的水平地面上,某时刻开始,受到的水平力F作用后,速度v随时间t变化关系如图所示,则下列说法正确的是( )| A. | 0~t2时间内,F的功率先增大后减小 | |
| B. | t2时刻F等于0 | |
| C. | t2~t3时间内F做正功 | |
| D. | t1~t3时间内,F先做正功后做负功,总功为0 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
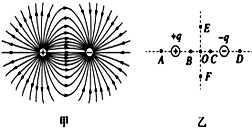
| A. | A、D两点场强大小相等,方向相反 | B. | E、O、F三点比较,O点电势最高 | ||
| C. | E、O、F三点比较,O点场强最强 | D. | B、O、C三点比较,O点场强最强 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 常温下,若将金属丝均匀拉长为原来的10倍,则电阻变为10R | |
| B. | 常温下,若将金属丝从中点对折起来,电阻变为$\frac{1}{2}$R | |
| C. | 给金属丝加热温度逐渐升高过程,任一状态下的 $\frac{U}{I}$ 比值一定不变 | |
| D. | 把金属丝温度降到很低时,电阻率会突然变为零的现象称为超导现象 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com