
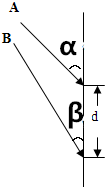
 如图,墙壁上落有两只飞镖,它们是从同一位置水平射出的.飞镖A与竖直墙壁成α角,飞镖B与竖直墙壁成β角;两者相距为d,假设飞镖的运动是平抛运动.求:
如图,墙壁上落有两只飞镖,它们是从同一位置水平射出的.飞镖A与竖直墙壁成α角,飞镖B与竖直墙壁成β角;两者相距为d,假设飞镖的运动是平抛运动.求:分析 (1)两只飞镖水平射出,都做平抛运动,水平方向的分运动是匀速直线运动,竖直方向的分运动是自由落体运动,根据速度的分解,用竖直方向的分速度分别表示出两个飞镖的初速度,由水平距离与初速度之比表示两个飞镖运动的时间、两个飞镖竖直距离之差等于d,即可求解水平距离.
(2)将飞镖的运动沿水平方向与竖直方向分解,写出飞镖的动能的表达式,确定动能最小的条件,然后即可求出;
(3)在(2)的条件下,将竖直方向的位移公式代入即可求出.
解答 解:(1)设水平距离为S,镖的初速度为v0,竖直分速度为vy,速度与竖直方向的夹角为θ.
则vy=v0cotθ=gt
v0=$\frac{S}{t}$
联立解得:t2=$\frac{Scotθ}{g}$
下落高度h=$\frac{1}{2}$gt2=$\frac{1}{2}$Scotθ
则由题有:hA=$\frac{1}{2}$S•cotα,
hB=$\frac{1}{2}$S•cotβ
又 hB-hA=d
解得:S=$\frac{2d}{cotβ-cotα}$
(2)设飞镖到达墙壁时的速度为v,则:
到达墙壁的动能:${E}_{k}=\frac{1}{2}m{v}^{2}=\frac{1}{2}m•\frac{{v}_{0}^{2}}{{sin}^{2}θ}$
由于:$\frac{{v}_{0}^{2}}{{sin}^{2}θ}$=$\frac{(\frac{S}{t})^{2}}{si{n}^{2}θ}$=$\frac{\frac{{S}^{2}}{\frac{S•cotθ}{g}}}{si{n}^{2}θ}$=$\frac{gS}{sinθcosθ}$
可知当sinθ•cosθ最大时,飞镖的动能最小,由三角函数的关系可知,sinθ•cosθ最大时θ=45°.
联立以上的方程,θ=45°时,得:${v}_{0}=\frac{S}{t}=\sqrt{gS}$=$\sqrt{\frac{2gd}{cotβ-cotα}}$
(3)在(2)的情况下,若飞镖不落地,则最小的高度:${h}_{min}=\frac{1}{2}g{t}^{2}$=$\frac{1}{2}g•\frac{Scot45°}{g}=\frac{1}{2}S$=$\frac{d}{cotβ-cotα}$
答:(1)射出点离墙壁的水平距离是$\frac{2d}{cotβ-cotα}$;
(2)若在该射出点水平射出飞镖C,要求它以最小动能击中墙壁,则C的初速度应为$\sqrt{\frac{2gd}{cotβ-cotα}}$;
(3)在第(2)问情况下,飞镖C与竖直墙壁的夹角是45°.射出点离地高度应满足h≥$\frac{d}{cotβ-cotα}$.
点评 该题将日常中常见的飞镖运动与平抛运动相结合进行考查,因涉及最小值问题,难度比较大.解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式灵活求解.


 名校课堂系列答案
名校课堂系列答案科目:高中物理 来源: 题型:选择题
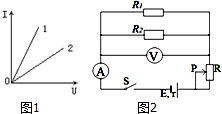 如图1所示为两电阻R1和R2的伏安特性曲线.将电阻R1和R2接入如图2所示电路中,电源内阻不可忽略,闭合开关s后,当滑动变阻器触片P向上移动时,则( )
如图1所示为两电阻R1和R2的伏安特性曲线.将电阻R1和R2接入如图2所示电路中,电源内阻不可忽略,闭合开关s后,当滑动变阻器触片P向上移动时,则( )| A. | 电流表示数变小 | |
| B. | 电压表示数增大 | |
| C. | 电源的总功率变小 | |
| D. | 电阻R1上的电流小于电阻R2上的电流 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
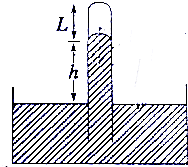 一端封闭的玻璃管倒插入水银槽中,管竖直放置时,管内水银面比管外高h(cm),上端空气柱长为L(cm),如图所示.已知大气压强为HcmHg,下列说法正确的是( )
一端封闭的玻璃管倒插入水银槽中,管竖直放置时,管内水银面比管外高h(cm),上端空气柱长为L(cm),如图所示.已知大气压强为HcmHg,下列说法正确的是( )| A. | 此时封闭气体的压强是(L+h)cmHg | B. | 此时封闭气体的压强是(H一h)cmHg | ||
| C. | 此时封闭气体的压强是(H+h)cmHg | D. | 此时封闭气体的压强是(H-L)cmHg |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
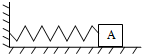 如图所示,一轻弹簧固定在墙上,另一端固定在物体A上,A放在光滑水平面上处于静止状态,现拉着A向右移动一段距离后松手,由松手到回到原位置过程中( )
如图所示,一轻弹簧固定在墙上,另一端固定在物体A上,A放在光滑水平面上处于静止状态,现拉着A向右移动一段距离后松手,由松手到回到原位置过程中( )| A. | 物体的加速度不断减小 | B. | 物体的加速度保持恒定 | ||
| C. | 物体的速度逐渐减小 | D. | 物体的速度先增大后减小 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,劲度系数为200N/m的弹簧秤拉着一个质量为3kg的物块在水平桌面上做匀速直线运动,已知弹簧的伸长量为6cm.(g=10N/kg)求:
如图所示,劲度系数为200N/m的弹簧秤拉着一个质量为3kg的物块在水平桌面上做匀速直线运动,已知弹簧的伸长量为6cm.(g=10N/kg)求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 瞬时速度,平均速度 | B. | 平均速度,瞬时速度 | ||
| C. | 瞬时速度,瞬时速度 | D. | 平均速度,平均速度 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com