
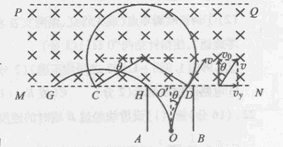
 =1x108C/kg、初速度v0=2x 105m/s的带正电粒子.忽略粒子重力、粒子间相互作用以及粒子在极板间飞行时极 板间的电压变化.sin30=0.5,sin37=0.6,sin45=
=1x108C/kg、初速度v0=2x 105m/s的带正电粒子.忽略粒子重力、粒子间相互作用以及粒子在极板间飞行时极 板间的电压变化.sin30=0.5,sin37=0.6,sin45= .
.
 =
=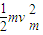 -
-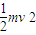
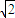 ×105m/s
×105m/s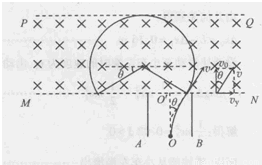 tm,由牛顿第二定律、平行四边形定则、几何关系及运动学公式得
tm,由牛顿第二定律、平行四边形定则、几何关系及运动学公式得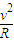
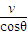
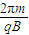
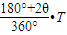
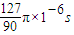 ≈4.43×10-6s
≈4.43×10-6s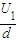
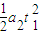
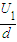
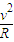
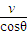
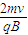
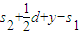
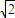 ×105m/s.
×105m/s.

科目:高中物理 来源: 题型:
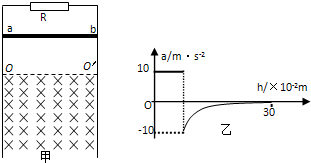 (2011?徐州一模)如图甲所示,两条足够长的光滑平行金属导轨竖直放置,导轨问距为L=1m,两导轨的,上端间接有电阻,阻值R=2Ω 虚线OO′下方是垂宣予导轨平面向里的匀强磁场,磁场磁感应强度为2T,现将质量m=0.1kg电阻不计的金届杆ab,从OO′上方某处由静止释放,金属杆在下落的过程中与导轨保持良好接触,且始终保持水平,不计导轨的电阻.已知金属杆下落0.3m的过程中加速度a与下落距离h的关系图象如图乙所示.求:
(2011?徐州一模)如图甲所示,两条足够长的光滑平行金属导轨竖直放置,导轨问距为L=1m,两导轨的,上端间接有电阻,阻值R=2Ω 虚线OO′下方是垂宣予导轨平面向里的匀强磁场,磁场磁感应强度为2T,现将质量m=0.1kg电阻不计的金届杆ab,从OO′上方某处由静止释放,金属杆在下落的过程中与导轨保持良好接触,且始终保持水平,不计导轨的电阻.已知金属杆下落0.3m的过程中加速度a与下落距离h的关系图象如图乙所示.求:查看答案和解析>>
科目:高中物理 来源: 题型:
| q |
| m |
| ||
| 2 |

查看答案和解析>>
科目:高中物理 来源:枣庄一模 题型:填空题
| q |
| m |
| ||
| 2 |

查看答案和解析>>
科目:高中物理 来源:2011-2012学年江苏省常州市高二(上)期末物理试卷(解析版) 题型:解答题
 如图甲所示,两条足够长的光滑平行金属导轨竖直放置,导轨问距为L=1m,两导轨的,上端间接有电阻,阻值R=2Ω 虚线OO′下方是垂宣予导轨平面向里的匀强磁场,磁场磁感应强度为2T,现将质量m=0.1kg电阻不计的金届杆ab,从OO′上方某处由静止释放,金属杆在下落的过程中与导轨保持良好接触,且始终保持水平,不计导轨的电阻.已知金属杆下落0.3m的过程中加速度a与下落距离h的关系图象如图乙所示.求:
如图甲所示,两条足够长的光滑平行金属导轨竖直放置,导轨问距为L=1m,两导轨的,上端间接有电阻,阻值R=2Ω 虚线OO′下方是垂宣予导轨平面向里的匀强磁场,磁场磁感应强度为2T,现将质量m=0.1kg电阻不计的金届杆ab,从OO′上方某处由静止释放,金属杆在下落的过程中与导轨保持良好接触,且始终保持水平,不计导轨的电阻.已知金属杆下落0.3m的过程中加速度a与下落距离h的关系图象如图乙所示.求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com