
 ��ͼ��ʾ���ռ�ֲ���������߽����ǿ�糡����ǿ�ų��������ǿ�糡���߽��ĵ��Ʋ�ΪU����ǿ����ˮƽ���ң������ΪL���м�������ǿ�ų��Ÿ�Ӧǿ�ȴ�СΪB������ֱֽ�����⣮�Ҳ���ǿ�ų��ĴŸ�Ӧǿ�ȴ�СΪ4B������ֱֽ�����һ������������ӣ�����Ϊm������q�������������ӵ糡���Եa���ɾ�ֹ��ʼ�˶��������м�ų���������Ҳ�ų�������ֻص���a�㣬Ȼ���ظ������˶����̣���
��ͼ��ʾ���ռ�ֲ���������߽����ǿ�糡����ǿ�ų��������ǿ�糡���߽��ĵ��Ʋ�ΪU����ǿ����ˮƽ���ң������ΪL���м�������ǿ�ų��Ÿ�Ӧǿ�ȴ�СΪB������ֱֽ�����⣮�Ҳ���ǿ�ų��ĴŸ�Ӧǿ�ȴ�СΪ4B������ֱֽ�����һ������������ӣ�����Ϊm������q�������������ӵ糡���Եa���ɾ�ֹ��ʼ�˶��������м�ų���������Ҳ�ų�������ֻص���a�㣬Ȼ���ظ������˶����̣������� ��1��������������ڵ糡�����ȼ���ֱ���˶�����ֱ����ų���������Բ���˶������������˶��Ĺ켣�����ݶ��ܶ������������������ڴų����˶������ʣ�
��2�������ڴų��������������䵱����������ţ�ٵڶ���������켣�İ뾶�����ݼ��ι�ϵ����м�ų�����Ŀ��ȣ�
��3��������ڵ糡���˶���ʱ�䣬����������δų����˶���ʱ�䣬����֮�ͼ��ɴ������Ӵ�O�㿪ʼ�˶�����һ�λص�O������ʱ�䣮
��� �⣺��1�����������ڵ糡�м��ٹ��̣��ɶ��ܶ����ã�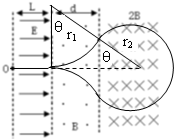
qU=$\frac{1}{2}m{v}^{2}$����v=$\sqrt{\frac{2qU}{m}}$
��2�������������ų���������Բ���˶��İ뾶�ֱ�Ϊr1��r2��
��qvB=m$\frac{{v}^{2}}{r}$�ã�r1=$\frac{m\sqrt{2qU}}{qB}$��r2=$\frac{m\sqrt{2qU}}{4qB}$=$\frac{1}{4}{r}_{1}$
�����������ӵ��˶��켣��ͼ�������켣Բ��������ų��߽�ɦȽǣ����ɼ���֪ʶ��
2��r1-r1cos�ȣ�=2r2cos��
��r1=4r2��
��ã�cos��=$\frac{4}{5}$����sin��=$\sqrt{1-\frac{{4}^{2}}{{5}^{2}}}=\frac{3}{5}$
��=37��=$\frac{37��}{180}$rad
���м�ų�����Ŀ���d=r1sin��=$\frac{3}{5}{r}_{1}=\frac{3m\sqrt{2qU}}{5qB}$
��3����t1��t2��t3�ֱ��ʾ�����ڵ糡���м�ų����ұߴų����˶���ʱ�䣬��
L=$\overline{v}{t}_{1}$=$\frac{v}{2}{t}_{1}$
�ã�t1=$2L\sqrt{\frac{m}{2qU}}$
vt2=r1•2��
vt3=r2•����+2�ȣ�
��ʱ��Ϊ��t=t1+t2+t3
�������ݵã�t=$2L\sqrt{\frac{m}{2qU}}$+$\frac{365��m}{360qB}$
�𣺣�1�����������ڴų����˶���������$\sqrt{\frac{2qU}{m}}$��
��2���м�ų�����Ŀ���d��$\frac{3m\sqrt{2qU}}{5qB}$��
��3���������Ӵ�O�㿪ʼ�˶�����һ�λص�O�����õ�ʱ��t��$2L\sqrt{\frac{m}{2qU}}$+$\frac{365��m}{360qB}$��
���� �����Ǵ�����������ϳ����˶������⣬����ؼ��ǻ������ӵ��˶��켣�����ü���֪ʶ���켣�뾶��


 ������ϵ�д�
������ϵ�д� �±�Сѧ��Ԫ�Բ���ϵ�д�
�±�Сѧ��Ԫ�Բ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
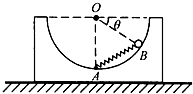 ��ͼ��ʾ���ڱڹ⻬���뾶ΪR�İ������������ڴֲڵ�ˮƽ���ϣ�OΪ���ģ���һ����ϵ��Ϊk���ᵯ��һ�˹̶��������ײ�A�㣬������һ��������Ϊm��С��������С��ֹ��B�㣮��֪OB��ˮƽ����ļн�Ϊ��=30�㣮����˵����ȷ���ǣ�������
��ͼ��ʾ���ڱڹ⻬���뾶ΪR�İ������������ڴֲڵ�ˮƽ���ϣ�OΪ���ģ���һ����ϵ��Ϊk���ᵯ��һ�˹̶��������ײ�A�㣬������һ��������Ϊm��С��������С��ֹ��B�㣮��֪OB��ˮƽ����ļн�Ϊ��=30�㣮����˵����ȷ���ǣ�������| A�� | ˮƽ������������ҵ�Ħ���� | B�� | �ᵯ�ɶ�С�����������СΪ$\frac{1}{2}$mg | ||
| C�� | ������С�����������СΪmg | D�� | ����ԭ��ΪR+$\frac{mg}{k}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
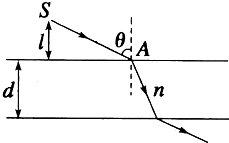 ��������Ϊn�����Ϊd�IJ���ƽ���Ϸ��Ŀ�������һ���ԴS����S�����Ĺ���SA������Ǧ����䵽�������ϱ��棬�������������±����������ͼ��ʾ�����ش˹��ߴ����Ĺ�ӹ�ԴS���������ϱ���Ĵ���ʱ�����ڲ������д���ʱ����ȣ����ԴS���������ϱ���Ĵ�ֱ����lӦ�Ƕ��٣�
��������Ϊn�����Ϊd�IJ���ƽ���Ϸ��Ŀ�������һ���ԴS����S�����Ĺ���SA������Ǧ����䵽�������ϱ��棬�������������±����������ͼ��ʾ�����ش˹��ߴ����Ĺ�ӹ�ԴS���������ϱ���Ĵ���ʱ�����ڲ������д���ʱ����ȣ����ԴS���������ϱ���Ĵ�ֱ����lӦ�Ƕ��٣��鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | �õ�Դ��ѹ�����ֵΪ6V | B�� | �õ�Դ��ѹ����ЧֵΪ6V | ||
| C�� | �õ�Դ��ѹ�����ֵΪ12V |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ�������������Ե����ͨ��������I������A��B��C��D��Ϊ��ȵ������Σ���ƽ���Ÿ�Ӧǿ�����������ҷ���ֱֽ��������ǣ�������
��ͼ��ʾ�������������Ե����ͨ��������I������A��B��C��D��Ϊ��ȵ������Σ���ƽ���Ÿ�Ӧǿ�����������ҷ���ֱֽ��������ǣ�������| A�� | A�� | B�� | B�� | C�� | C�� | D�� | D�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ��ʽF=G$\frac{{m}_{1}{m}_{2}}{{x}^{2}}$ֻ�����ڼ�������������֮����������� | |
| B�� | ���������ľ���r�ܽ�ʱ����������Ѳ����������������ʲ����ù�ʽF=G$\frac{{m}_{1}{m}_{2}}{{x}^{2}}$������ | |
| C�� | �������������ܵ�������������������ù�ʽF=G$\frac{{m}_{1}{m}_{2}}{{x}^{2}}$���� | |
| D�� | �ڽ����ڣ�ͬѧ֮��Ҳ���������� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
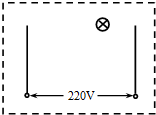 ����¥�������������Ĺ��ܣ����ʱ�������������Ϳ��������ڰ��켴ʹ��������Ҳû��Ӧ�����Ŀ��Ƶ����н����������������غ�������أ�����Щ�����������źţ�ͨ��һ�����ţ�ѡ����š��������š����š�����·����ִ�е�·����ͼ�е�����ڻ������ִ��������ؿ��Ƶ�¥���Ƶ�·ͼ��
����¥�������������Ĺ��ܣ����ʱ�������������Ϳ��������ڰ��켴ʹ��������Ҳû��Ӧ�����Ŀ��Ƶ����н����������������غ�������أ�����Щ�����������źţ�ͨ��һ�����ţ�ѡ����š��������š����š�����·����ִ�е�·����ͼ�е�����ڻ������ִ��������ؿ��Ƶ�¥���Ƶ�·ͼ���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
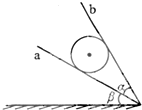 ��ͼ��ʾ������Ϊm�ĸ���ֹ�����⻬ľ��a��b֮�䣬��֪��ľ��ļнǦ�=30�㣬aľ����ˮƽ��ļнǦ�=30�㣬������a��b���ѹ����СFa��Fb�ֱ��ǣ�������
��ͼ��ʾ������Ϊm�ĸ���ֹ�����⻬ľ��a��b֮�䣬��֪��ľ��ļнǦ�=30�㣬aľ����ˮƽ��ļнǦ�=30�㣬������a��b���ѹ����СFa��Fb�ֱ��ǣ�������| A�� | Fa=mg��Fb=mg | B�� | Fa=$\sqrt{3}$mg��Fb=$\frac{\sqrt{3}}{2}$mg | C�� | Fa=$\frac{\sqrt{3}}{2}$mg��Fb=$\sqrt{3}$mg | D�� | Fa=$\sqrt{3}$mg��Fb=mg |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com