
| A. | 角速度之比为2:1 | B. | 向心加速度之比为4:1 | ||
| C. | 周期之比为1:8 | D. | 向心力之比为16:1 |
分析 卫星绕地球做匀速圆周运动,万有引力提供向心力,应用牛顿第二定律求出角速度、向心加速度、周期、向心力,然后求出其比值.
解答 故解:卫星绕地球做匀速圆周运动,万有引力提供向心力,由牛顿第二定律得:
G$\frac{Mm}{{r}^{2}}$=m$\frac{{v}^{2}}{r}$,解得:r=$\frac{GM}{{v}^{2}}$,卫星的线速度v减小为原来的$\frac{1}{2}$,则:r′=4r;
A、由牛顿第二定律得:G$\frac{Mm}{{r}^{2}}$=mω2r,解得:ω=$\sqrt{\frac{GM}{{r}^{3}}}$,则:$\frac{ω}{ω′}$=$\sqrt{\frac{r{′}^{3}}{{r}^{3}}}$=$\frac{8}{1}$,故A错误;
B、由牛顿第二定律得:G$\frac{Mm}{{r}^{2}}$=ma,解得:a=$\frac{GM}{{r}^{2}}$,则:$\frac{a}{a′}$=$\frac{r{′}^{2}}{{r}^{2}}$=$\frac{16}{1}$,故B错误;
C、由牛顿第二定律得:G$\frac{Mm}{{r}^{2}}$=m($\frac{2π}{T}$)2r,解得:T=2π$\sqrt{\frac{{r}^{3}}{GM}}$,则:$\frac{T}{T′}$=$\sqrt{\frac{{r}^{3}}{{r′}^{3}}}$=$\frac{1}{8}$,故C正确;
D、万有引力提供向心力:F=G$\frac{Mm}{{r}^{2}}$,则:$\frac{F}{F′}$=$\frac{r{′}^{2}}{{r}^{2}}$=$\frac{16}{1}$,故D正确;
故选:CD;
点评 本题考查了万有引力定律的应用,知道地球表面的物体受到的重力等于万有引力、知道万有引力提供向心力,应用牛顿第二定律即可解题.


科目:高中物理 来源: 题型:填空题
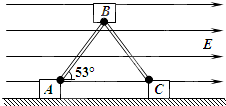 如图所示,两个长均为L的轻质杆,通过A、B、C上垂直纸面的转动轴与A、B、C三个物块相连,整体处于竖直面内.A、C为两个完全相同的小物块,B物块的质量与A小物块的质量之比为2:1,三个物块的大小都可忽略不计.A、C两物块分别带有+q、-q的电荷量,并置于绝缘水平面上,在水平面上方有水平向右的匀强电场,场强为E,物块间的库仑力不计.当AB、BC与水平面间的夹角均为53°时,整体恰好处于静止状态,一切摩擦均不计,并且在运动过程中无内能产生,重力加速度为g,(sin53°=0.8,cos53°=0.6),则B物块的质量为$\frac{8Eq}{3g}$;若将B物块略向下移动一些,并由静止释放,则B物块到达地面前瞬时速度的大小为$\sqrt{gL}$.
如图所示,两个长均为L的轻质杆,通过A、B、C上垂直纸面的转动轴与A、B、C三个物块相连,整体处于竖直面内.A、C为两个完全相同的小物块,B物块的质量与A小物块的质量之比为2:1,三个物块的大小都可忽略不计.A、C两物块分别带有+q、-q的电荷量,并置于绝缘水平面上,在水平面上方有水平向右的匀强电场,场强为E,物块间的库仑力不计.当AB、BC与水平面间的夹角均为53°时,整体恰好处于静止状态,一切摩擦均不计,并且在运动过程中无内能产生,重力加速度为g,(sin53°=0.8,cos53°=0.6),则B物块的质量为$\frac{8Eq}{3g}$;若将B物块略向下移动一些,并由静止释放,则B物块到达地面前瞬时速度的大小为$\sqrt{gL}$.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,在水平向右的均强电场中固定一个斜面体,斜面体的高为H,斜面光滑且倾角为α,一质量为m的物块从斜面的底端以初速度v0沿斜面向上滑动,物块带电量为+q,电场强度大小E=$\frac{mgtanα}{q}$,求:
如图所示,在水平向右的均强电场中固定一个斜面体,斜面体的高为H,斜面光滑且倾角为α,一质量为m的物块从斜面的底端以初速度v0沿斜面向上滑动,物块带电量为+q,电场强度大小E=$\frac{mgtanα}{q}$,求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
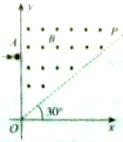 如图所示,有一平行纸面的直角坐标系xOy,坐标轴Oy垂直于水平金属板,在其POy区域内有垂直纸面向外,磁感应强度为B的匀强磁场,磁场边界OP与x轴正方向夹角为30°;POx区域为无场区.一质量为m,带电荷量为+q的粒子沿从A(0,b)点垂直于y轴进入第Ⅰ象限POy区域,经OP上某点离开磁场,最后沿与x轴正向成60°角的方向离开第Ⅰ象限,不计粒子重力,求:粒子进入磁场的初速度大小.
如图所示,有一平行纸面的直角坐标系xOy,坐标轴Oy垂直于水平金属板,在其POy区域内有垂直纸面向外,磁感应强度为B的匀强磁场,磁场边界OP与x轴正方向夹角为30°;POx区域为无场区.一质量为m,带电荷量为+q的粒子沿从A(0,b)点垂直于y轴进入第Ⅰ象限POy区域,经OP上某点离开磁场,最后沿与x轴正向成60°角的方向离开第Ⅰ象限,不计粒子重力,求:粒子进入磁场的初速度大小.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 一个轻质弹簧的劲度系数为k,一端固定,另一端在力的作用下发生的形变量为x,已知克服弹力所做的功等于弹簧弹性势能的增加量.(以上过程均在弹簧的弹性限度内)
一个轻质弹簧的劲度系数为k,一端固定,另一端在力的作用下发生的形变量为x,已知克服弹力所做的功等于弹簧弹性势能的增加量.(以上过程均在弹簧的弹性限度内)查看答案和解析>>
科目:高中物理 来源: 题型:选择题
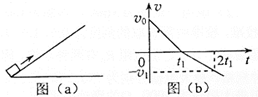 如图(a),一物块在t=0时刻滑上一固定斜面,其运动的v?t图线如图(b)所示.若重力加速度及图中的v0、v1、t1均为己知量,则不可求出( )
如图(a),一物块在t=0时刻滑上一固定斜面,其运动的v?t图线如图(b)所示.若重力加速度及图中的v0、v1、t1均为己知量,则不可求出( )| A. | 斜面的倾角 | B. | 物块的质量 | ||
| C. | 物块与斜面间的动摩擦因数 | D. | 物块沿斜面向上滑行的最大高度 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题

| 计数点 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| h/m | 0.124 | 0.194 | 0.279 | 0.380 | 0.497 | 0.630 | 0.777 |
| v/(m•s-1) | 1.94 | 2.33 | 2.73 | 3.13 | 3.50 | ||
| v2/(m2•s-2) | 3.76 | 5.43 | 7.45 | 9.80 | 12.25 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 远距离输电线路示意图如图所示,变压器均为理想变压器,发电机的输出电压及输电线的电阻均不变.则( )
远距离输电线路示意图如图所示,变压器均为理想变压器,发电机的输出电压及输电线的电阻均不变.则( )| A. | 用户负载增加时,升压变压器的原线圈中电流不变 | |
| B. | 降压变压器的原线圈中电流较小,用较粗的导线绕制成 | |
| C. | 因为先升压后又要降压,所以不用变压器直接输电更节约电能 | |
| D. | 当用户用电器的总电阻增大时,输电线上损失的功率减小 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com