
分析 根据万有引力定律公式,结合轨道半径的变化得出万有引力大小的变化,根据万有引力提供向心力,得出周期与轨道半径的关系,从而分析求解.
解答 解:根据万有引力定律公式得,F=$G\frac{Mm}{{R}^{2}}$,
当半径变为4R时,F′=$G\frac{Mm}{(4R)^{2}}$,
所以F′=$\frac{1}{16}F$.
匀速圆周运动中,引力提供向心力:$G\frac{Mm}{{R}^{2}}=mR\frac{4{π}^{2}}{{T}^{2}}$,
当半径变为4R时,$G\frac{Mm}{(4R)^{2}}=m•4R•\frac{4{π}^{2}}{T{′}^{2}}$,
联立解得T′=8T 即那时地球上“一年”相当于现在的8年.
答:太阳对地球的引力F′是F的$\frac{1}{16}$倍,那时地球上的“一年”(绕太阳公转一周的时间)相当于现在的8年.
点评 解决本题的关键掌握万有引力提供向心力这一重要理论,知道周期与轨道半径的关系,难度不大.


 阅读快车系列答案
阅读快车系列答案科目:高中物理 来源: 题型:填空题
 一定质量的理想气体,依次进行三个不同温度的等温变化,其1、2、3过程的p-V图如图所示.由图可知,气体在这三个过程中的温度关系为:T1<T2,T3>T1(选填“>”、“<”或“=”)
一定质量的理想气体,依次进行三个不同温度的等温变化,其1、2、3过程的p-V图如图所示.由图可知,气体在这三个过程中的温度关系为:T1<T2,T3>T1(选填“>”、“<”或“=”)查看答案和解析>>
科目:高中物理 来源: 题型:选择题
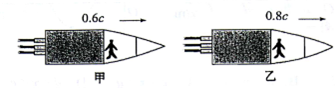 如图所示,质量与身高均相同的甲、乙两人分别乘坐速度为0.6c和0.8c(c为光速)的飞船同向运动.则下列说法中正确的是( )
如图所示,质量与身高均相同的甲、乙两人分别乘坐速度为0.6c和0.8c(c为光速)的飞船同向运动.则下列说法中正确的是( )| A. | 乙观察到甲身高变高 | |
| B. | 甲观察到乙身高变低 | |
| C. | 若甲向乙挥手,则乙观察到甲动作变快 | |
| D. | 若甲向乙发出一束光进行联络,则乙观察到该光束的传播速度为c |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 它们受到地球的引力之比为FA:FB=1:1 | |
| B. | 它们的运行速度大小之比为vA:vB=1:$\sqrt{2}$ | |
| C. | 它们的运行周期之比为TA:TB=$\sqrt{2}$:1 | |
| D. | 它们的运行角速度之比为ωA:ωB=3$\sqrt{2}$:1 |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
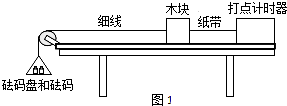

查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 木星的质量为$\frac{g{R}^{2}}{G}$ | B. | 木星的平均密度为$\frac{3g}{4pGR}$ | ||
| C. | 该卫星运动的周期为4p$\sqrt{\frac{2R}{g}}$ | D. | 该卫星运动的周期为4p$\sqrt{\frac{R}{g}}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 一矩形线圈,面积是0.05m2,共10匝,线圈电阻为2Ω,外接电阻为R=8Ω,线圈在磁感应强度为$B=\frac{{\sqrt{2}}}{π}T$的匀强磁场中,以300r/min的转速绕垂直于磁感线的轴匀速转动,t=0时刻,线圈在图示位置,求:
一矩形线圈,面积是0.05m2,共10匝,线圈电阻为2Ω,外接电阻为R=8Ω,线圈在磁感应强度为$B=\frac{{\sqrt{2}}}{π}T$的匀强磁场中,以300r/min的转速绕垂直于磁感线的轴匀速转动,t=0时刻,线圈在图示位置,求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
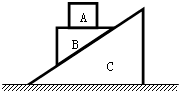 如图,光滑斜面C静止在粗糙的水平地面上,质量均为m的滑块A、B叠放在一起后由静止开始下滑,此过程中斜面保持静止.则下列说法正确的是( )
如图,光滑斜面C静止在粗糙的水平地面上,质量均为m的滑块A、B叠放在一起后由静止开始下滑,此过程中斜面保持静止.则下列说法正确的是( )| A. | A对B的压力等于mg | B. | A、B 间没有摩擦力的作用 | ||
| C. | 地面对C的摩擦力方向水平向左 | D. | 若将A撤去,则B下滑的加速度变小 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com