
 有两个用特殊材料做成的两个物体A和B,质量都为m;它们之间存在一种相互作用,这个作用力F与它们间的距离x的关系为F=ρ(x0-x),其中k、x0为已知常数,当两者间距离x<x0时,这个作用表现为斥力,当x>x0时,这个作用表现为引力,当x=x0时,作用力为零.现将物体B固定在水平地面上,再将A移到B的正上方,最终A能静止于B的正上方的某处,试求:(已知重力加速度大小为g)
有两个用特殊材料做成的两个物体A和B,质量都为m;它们之间存在一种相互作用,这个作用力F与它们间的距离x的关系为F=ρ(x0-x),其中k、x0为已知常数,当两者间距离x<x0时,这个作用表现为斥力,当x>x0时,这个作用表现为引力,当x=x0时,作用力为零.现将物体B固定在水平地面上,再将A移到B的正上方,最终A能静止于B的正上方的某处,试求:(已知重力加速度大小为g) 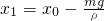
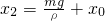
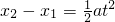
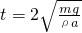
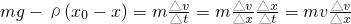
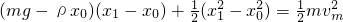
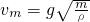
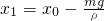 ;
;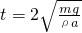 ,B开始离开地面;
,B开始离开地面;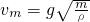 .
.

 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中物理 来源: 题型:
查看答案和解析>>
科目:高中物理 来源: 题型:
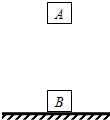
 (2011?江苏模拟)有两个用特殊材料做成的两个物体A和B,质量都为m;它们之间存在一种相互作用,这个作用力F与它们间的距离x的关系为F=ρ(x0-x),其中k、x0为已知常数,当两者间距离x<x0时,这个作用表现为斥力,当x>x0时,这个作用表现为引力,当x=x0时,作用力为零.现将物体B固定在水平地面上,再将A移到B的正上方,最终A能静止于B的正上方的某处,试求:(已知重力加速度大小为g)
(2011?江苏模拟)有两个用特殊材料做成的两个物体A和B,质量都为m;它们之间存在一种相互作用,这个作用力F与它们间的距离x的关系为F=ρ(x0-x),其中k、x0为已知常数,当两者间距离x<x0时,这个作用表现为斥力,当x>x0时,这个作用表现为引力,当x=x0时,作用力为零.现将物体B固定在水平地面上,再将A移到B的正上方,最终A能静止于B的正上方的某处,试求:(已知重力加速度大小为g) 查看答案和解析>>
科目:高中物理 来源:江苏模拟 题型:问答题
查看答案和解析>>
科目:高中物理 来源:2011年江苏省高考物理模拟试卷(三)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com