
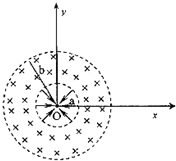
 如图所示,半径分别为a、b的两同心虚线圆所围区域存在垂直纸面向里的匀强磁场,在小圆内沿径向存在电场,电场方向指向圆心O,小圆周与金属球间的电势差为U.在O处固定一个半径很小(可忽略不计)的金属球,设有一个带负电的粒子从金属球表面沿x轴正方向以很小的初速度逸出,粒子质量为m,电荷量为q.不计粒子的重力,忽略粒子逸出的初速度,求:
如图所示,半径分别为a、b的两同心虚线圆所围区域存在垂直纸面向里的匀强磁场,在小圆内沿径向存在电场,电场方向指向圆心O,小圆周与金属球间的电势差为U.在O处固定一个半径很小(可忽略不计)的金属球,设有一个带负电的粒子从金属球表面沿x轴正方向以很小的初速度逸出,粒子质量为m,电荷量为q.不计粒子的重力,忽略粒子逸出的初速度,求:分析 (1)根据动能定理,通过末动能求出加速电压的大小.
(2)根据洛伦兹力提供向心力,根据牛顿第二定律求出粒子在磁场中运动的轨道半径的表达式,要使粒子不能到达大圆周,其最大的圆半径为轨迹圆与大圆周相切.
(3)根据题目给定的条件,画出带电粒子运动的轨迹,从而确定粒子在磁场中转过φ=270°,然后沿半径进入电场减速到达金属球表面,再经电场加速原路返回磁场,如此重复,恰好经过4个回旋后,沿与原出射方向相反的方向回到原出发点.
解答 解:(1)粒子在电场中加速,根据动能定理得:$qU=\frac{1}{2}m{v^2}$,所以$v=\sqrt{\frac{2qU}{m}}$
(2)粒子进入磁场后,受洛伦兹力做匀速圆周运动$qvB=m\frac{v^2}{r}$,要使粒子不能到达大圆周,其最大的圆半径为轨迹圆与大圆周相切,如图.从而有$\sqrt{{a^2}+{r^2}}=b-r$,所以$r=\frac{{{b^2}-{a^2}}}{2b}$,故$B=\frac{2b}{{{b^2}-{a^2}}}\sqrt{\frac{2mU}{q}}$.
(3)由图可知$tanθ=\frac{r}{a}=\frac{{{b^2}-{a^2}}}{2ab}=1$,所以θ=45°.粒子在磁场中转270°,然后沿半径进入电场减速到达金属球表面,再经电场加速原路返回磁场,如此重复,恰好经过4个回旋后,沿与原出射方向相反的方向回到原出发点.
因为$T=\frac{2πm}{qB}$,所以粒子在磁场中运动时间$t=4×\frac{3}{4}T=\frac{{3π({b^2}-{a^2})}}{b}\sqrt{\frac{m}{2qU}}$.
答:(1)粒子到达小圆周上时的速度为$\sqrt{\frac{2qU}{m}}$;
(2)粒子以(1)中的速度进入两圆间的磁场中,当磁感应强度超过某一临界值时,粒子将不能到达大圆周,此临界值为$\frac{2b}{{{b^2}-{a^2}}}\sqrt{\frac{2mU}{q}}$;
(3)要粒子恰好第一次沿逸出方向的反方向回到原出发点,粒子需经过4次回旋;粒子在磁场中运动的时间为$\frac{{3π({b^2}-{a^2})}}{b}\sqrt{\frac{m}{2qU}}$.
点评 本题粒子在有圆形边界的磁场做匀速圆周运动的问题,画出轨迹,根据几何知识分析临界条件,求半径和圆心角是常用的思路.


 智慧小复习系列答案
智慧小复习系列答案科目:高中物理 来源: 题型:解答题
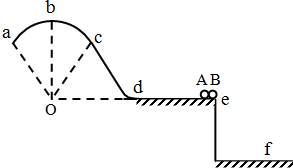 如图,竖直固定轨道abcd段光滑,长为L=1.0m的平台de段粗糙,abc段是以O为圆心的圆弧.小球A和B紧靠一起静止于e处,B的质量是A的4倍.两小球在内力作用下突然分离,A分离后向左始终沿轨道运动,小球A与de段的动摩擦因数μ=0.2,到b点时轨道对A的支持力等于A的重力的$\frac{3}{5}$;B分离后平抛落到f点,f到平台边缘的水平距离s=0.4m,平台高h=0.8m,g取10m/s2.求:
如图,竖直固定轨道abcd段光滑,长为L=1.0m的平台de段粗糙,abc段是以O为圆心的圆弧.小球A和B紧靠一起静止于e处,B的质量是A的4倍.两小球在内力作用下突然分离,A分离后向左始终沿轨道运动,小球A与de段的动摩擦因数μ=0.2,到b点时轨道对A的支持力等于A的重力的$\frac{3}{5}$;B分离后平抛落到f点,f到平台边缘的水平距离s=0.4m,平台高h=0.8m,g取10m/s2.求:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 只要技术可行,物体的温度可降至-274℃ | |
| B. | 物体从单一热源吸收的热量可全部用于做功 | |
| C. | 压缩气体总能使气体的温度升高 | |
| D. | 控制液面上方饱和汽的体积不变,升高温度,达到平衡后该饱和气压将增大 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 英国物理学家焦耳在热学、电磁学等方面做出了杰出贡献,成功地发现了焦耳定律 | |
| B. | 德国天文学家开普勒对他导师第谷观测的行星数据进行多年研究,得出了万有引力定律 | |
| C. | 英国物理学家卡文迪许利用卡文迪许扭秤首先较准确的测定了静电力常量 | |
| D. | 古希腊学者亚里士多德认为物体下落快慢由它们的重量决定,伽利略在他的《两种新科学的对话》中利用逻辑推断使亚里士多德的理论陷入了困境 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题

| A. | 48次/min,25mm/s | B. | 75次/min,25mm/s | C. | 75次/min,45mm/s | D. | 48次/min,36mm/s |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,两块相同的金属板正对着水平放置,电压U时,一个质量为m、电荷量为+q的带电粒子,以水平速度v0从A点射入电场,经过一段时间后从B点射出电场,A、B问的水平距离为L.不计重力影响.求
如图所示,两块相同的金属板正对着水平放置,电压U时,一个质量为m、电荷量为+q的带电粒子,以水平速度v0从A点射入电场,经过一段时间后从B点射出电场,A、B问的水平距离为L.不计重力影响.求查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 磁感线上每一点的切线方向 | B. | 小磁针北极受力的方向 | ||
| C. | 小磁针静止时北极所指的方向 | D. | 磁铁内部N极到S极的方向 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com