

分析 (1、2)先有动能定理求出进入磁场时的速度,导体棒进入磁场时金属杆切割磁感线,产生感应电流.由法拉第定律和欧姆定律可求得感应电流大小,由右手定则判断出感应电流方向;
(3)设导体杆在磁场中运动的时间为t,求出产生的感应电动势的平均值,根据欧姆定律求出电流的平均值,进而求出电量;
(4)由牛顿第二定律求出导体杆到达轨道最高点时的速度,由机械能守恒定律求出金属杆穿出磁场时的速度;
(5)回路中机械能转化为内能,根据能量守恒定律求出电路中产生的焦耳热.
解答 解:(1)设导体杆在F的作用下运动至磁场的左边界时的速度为v1,
由动能定理得:(F-μmg)s=$\frac{1}{2}$mv12-0,
解得:v1=6m/s
(2)导杆刚进入磁场时产生的感应电动势为:E=Blv1,
此时通过导体杆的电流大小为:I=$\frac{E}{R+r}$,
代入数据解得:I=3.6A,
由右手定则可知,电流的方向为由b指向a;
(3)设导体杆在磁场中运动的时间为 t,产生的感应电动势的平均值为$\overline{E}$,
则由法拉第电磁感应定律有 $\overline{E}=\frac{△∅}{t}=\frac{BLd}{t}$
通过电阻 R 的感应电流的平均值为$\overline{I}=\frac{\overline{E}}{R+r}$
通过电阻 R 的电荷量 q=$\overline{I}t$=0.6C
(4)设导体离开磁场时的速度为v2,运动到圆轨道最高点的速度为v3,
因导杆恰好能以最小速度通过圆轨道最高点,由牛顿第二定律得:mg=m$\frac{{{v}_{3}}^{2}}{{R}_{0}}$,
解得:v3=$\sqrt{5}$m/s
导体杆从MN′到PP′的过程,由机械能守恒定律得:$\frac{1}{2}$mv22=$\frac{1}{2}$mv32+mg•2R0,
解得 v2=5.0m/s;
(5)由能量守恒定律得:导体杆穿过磁场的过程中损失的机械能:△E=$\frac{1}{2}$mv12-$\frac{1}{2}$mv22,
导体杆穿过磁场的过程中整个电路产生的焦耳热为:Q=△E-μmgd,
解得:Q=0.94J;
答:(1)导体杆刚进入磁场时速度为6m/s;
(2)导体杆刚进入磁场时,通过导体杆上的电流大小为3.6A,方向由b指向a;
(3)导体杆穿过磁场的过程中通过电阻R上的电荷量为0.6C;
(4)杆出磁场瞬间速度为5.0m/s,在半圆轨道最高点速度为$\sqrt{5}$m/s;
(5)导体杆穿过磁场的过程中整个电路中产生的焦耳热为0.94J.
点评 本题首先要分析导体棒的运动过程,分三个子过程进行研究;其次要掌握三个过程遵守的规律,运用动能定理、能量守恒、牛顿第二定律、机械能守恒等联合求解.


科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
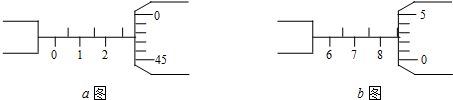
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
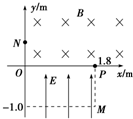 如图所示,在直角坐标系的第Ⅰ象限存在垂直纸面向里的匀强磁场,第Ⅳ象限分布着竖直向上的匀强电场,场强E=4.0×103 V/m,现从图中M(1.8,-1.0)点由静止释放一比荷$\frac{q}{m}$=2×105 C/kg的带正电的粒子,该粒子经过电场加速后经x轴上的P点进入磁场,在磁场中运动一段时间后经y轴上的N(0,0.6)点离开磁场.不计重力,问:
如图所示,在直角坐标系的第Ⅰ象限存在垂直纸面向里的匀强磁场,第Ⅳ象限分布着竖直向上的匀强电场,场强E=4.0×103 V/m,现从图中M(1.8,-1.0)点由静止释放一比荷$\frac{q}{m}$=2×105 C/kg的带正电的粒子,该粒子经过电场加速后经x轴上的P点进入磁场,在磁场中运动一段时间后经y轴上的N(0,0.6)点离开磁场.不计重力,问:查看答案和解析>>
科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:解答题
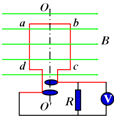 如图所示,为一交流发电机构造示意图,矩形线圈 abcd,已知ad=L1,ab=L2,匝数为n,线圈绕OO′轴在磁感应强度为B的匀强磁场中以角速度ω匀速转动,线圈电阻为r,外电路电阻为R,求:
如图所示,为一交流发电机构造示意图,矩形线圈 abcd,已知ad=L1,ab=L2,匝数为n,线圈绕OO′轴在磁感应强度为B的匀强磁场中以角速度ω匀速转动,线圈电阻为r,外电路电阻为R,求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
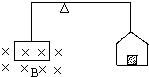 如图,当左边的线圈通以逆时针电流I时,天平恰好平衡,此时天平右边的砝码为m,若改为顺时针方向的电流且大小不变,则需在天平右边增加△m的砝码,通电线圈受到磁场力大小为( )
如图,当左边的线圈通以逆时针电流I时,天平恰好平衡,此时天平右边的砝码为m,若改为顺时针方向的电流且大小不变,则需在天平右边增加△m的砝码,通电线圈受到磁场力大小为( )| A. | $\frac{△mg}{2}$ | B. | (m+△m)g | C. | △mg | D. | $\frac{(m+△m)g}{2}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 在如图所示的电路中,电源电动势为E,内阻为r,电表均为理想电表,当滑片P向右移动时,两电表读数的变化是( )
在如图所示的电路中,电源电动势为E,内阻为r,电表均为理想电表,当滑片P向右移动时,两电表读数的变化是( )| A. | 电流表示数变大,电压表示数变大 | B. | 电流表示数变小,电压表示数变大 | ||
| C. | 电流表示数变大,电压表示数变小 | D. | 电流表示数变小,电压表示数变小 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com