
| A. | “天宫一号”的向心加速度与地球同步卫星的向心加速度之比为$\frac{{{T}_{0}}^{2}}{{T}^{2}}$ | |
| B. | “天宫一号”的角速度与地球同步卫星的角速度之比为$\frac{T}{{T}_{0}}$ | |
| C. | “天宫一号”的线速度与地球同步卫星的线速度之比为$(\frac{T}{{T}_{0}})^{\frac{1}{2}}$ | |
| D. | “天宫一号”的轨道半径与地球同步卫星的轨道半径之比为($\frac{{T}^{2}}{{{T}_{0}}^{2}}$)${\;}^{\frac{1}{3}}$ |
分析 根据万有引力提供向心力得出周期与轨道半径的关系式,结合周期之比得出轨道半径之比,再通过角速度、线速度、向心加速度的表达式,结合轨道半径之比求出各个物理量之比.
解答 解:A、根据$G\frac{Mm}{{r}^{2}}=ma$得,a=$\frac{GM}{{r}^{2}}$,可知加速度之比为$(\frac{{{T}_{0}}^{2}}{{T}^{2}})^{\frac{2}{3}}$,故A正确.
B、根据$G\frac{Mm}{{r}^{2}}=mr{ω}^{2}$得,$ω=\sqrt{\frac{GM}{{r}^{3}}}$,轨道半径之比为$(\frac{{T}^{2}}{{{T}_{0}}^{2}})^{\frac{1}{3}}$,则角速度之比为$\frac{{T}_{0}}{T}$,故B错误.
C、根据$G\frac{Mm}{{r}^{2}}=m\frac{{v}^{2}}{r}$得,$v=\sqrt{\frac{GM}{r}}$,则线速度之比为$(\frac{{T}^{2}}{{T}_{0}})^{\frac{1}{6}}$,故C错误.
D、根据$G\frac{Mm}{{r}^{2}}=mr\frac{4{π}^{2}}{{T}^{2}}$得,轨道半径r=$\root{3}{\frac{GM{T}^{2}}{4{π}^{2}}}$,天宫一号和同步卫星的周期之比为T:T0,则轨道半径之比为$(\frac{{T}^{2}}{{{T}_{0}}^{2}})^{\frac{1}{3}}$,故D正确.
故选:D.
点评 解决本题的关键知道卫星做圆周运动向心力的来源,结合牛顿第二定律进行求解,通过周期之比得出轨道半径之比是关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中物理 来源: 题型:选择题
| A. | 曲线运动是一种变速运动 | |
| B. | 做曲线运动的物体合外力一定不为零 | |
| C. | 做曲线运动的物体所受的合外力一定是变化的 | |
| D. | 曲线运动可能是一种匀变速运动 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 同步卫星的经纬度都相同 | |
| B. | 同步卫星的运行周期恒定不变,等于地球自转周期 | |
| C. | 同步卫星距地球的高度都相同 | |
| D. | 同步卫星的运行速度小于地球第一宇宙速度 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 如图所示,质量为m=l kg的物体静止在倾角为α=37°的粗糙斜面体上,两者一起向右做匀速直线运动,取g=10m/s2,则在通过水平位移x=1m的过程中:
如图所示,质量为m=l kg的物体静止在倾角为α=37°的粗糙斜面体上,两者一起向右做匀速直线运动,取g=10m/s2,则在通过水平位移x=1m的过程中:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | an=$\frac{{v}^{2}}{r}$ | B. | an=v2r | C. | an=$\frac{{ω}^{2}}{r}$ | D. | an=ω2r |
查看答案和解析>>
科目:高中物理 来源:2017届江西省赣州市十三县十四校高三上学期期中联考物理试卷(解析版) 题型:选择题
如图所示,有三个质量相等,分别带正电、负电和不带电的小球,从平行板电场左端的中点P以相同的初速度沿水平方向垂直于电场方向进入电场,它们分别落在A、B、C三点,可以判断( )
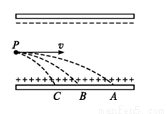
A.小球A带正电,B不带电,C带负电
B.三个小球在电场中运动时间相等
C.三个小球到达极板时的动能EkA<EkB<EkC
D.三个小球在电场中运动的加速度aA>aB>aC
查看答案和解析>>
科目:高中物理 来源:2016-2017学年江西赣州十三县十四校高一上期中考物理卷(解析版) 题型:选择题

A. 绳子的拉力大小小于A的重力大小
B. 绳子的拉力大小等于A、B重力大小之和
C. 物块B对物块A的支持力为零
D. 物块A对物块B的压力不为零
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com