
 ��ͼ��ʾ��һ�����쳤������ϸ��������ΪL��һ�˹̶���O�㣬��һ��ϵһ����Ϊm��С��С����O������ֱƽ������Բ���˶������ƿ�����������
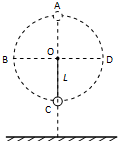
��ͼ��ʾ��һ�����쳤������ϸ��������ΪL��һ�˹̶���O�㣬��һ��ϵһ����Ϊm��С��С����O������ֱƽ������Բ���˶������ƿ��������������� ��1��С��ͨ����ߵ�ʱ������С������F�������ĺ����ṩ����������F=0ʱ���ٶ���С��
��2����С��ǡ��ͨ����ߵ�${v}_{A}=\sqrt{gL}$�����ݻ�е���غ㶨�����BD���ٶȣ��ٸ����˶�ѧ������ʽ���ʱ��
��3��С���˶�����ߵ�ʱ��������СֵΪmg������ţ�ٵڶ��������С����ߵ����С�ٶȣ�����ߵ㵽��͵㣬���û�е���غ���ʽ������⣮
��� �⣺��1����ͨ����ߵ�ʱ���ٶ�Ϊv��F+mg=m$\frac{{v}^{2}}{L}$
F=$\frac{{mv}^{2}}{L}-mg$
������FΪ��ʱ���ٶ�v����СֵΪ$\sqrt{gL}$
��2����С��ǡ��ͨ����ߵ�${v}_{A}=\sqrt{gL}$���ɻ�е���غ�
$\frac{1}{2}m{{v}_{B}}^{2}=\frac{1}{2}m{{v}_{A}}^{2}+mgL$
��ã�${v}_{B}={v}_{D}=\sqrt{3gL}$
��B�㡢D��С��ֱ���ֱ������ֱ���ף���
��t=$\frac{2{v}_{B}}{g}=\frac{2{v}_{D}}{g}$=$\frac{2\sqrt{3gL}}{g}$
��3��С���˶�����ߵ�A���Ͽ���ƽ���˶�����
$h+L=\frac{1}{2}g{{t}_{A}}^{2}$
xA=vAtA
С���˶�����͵�C���Ͽ���ƽ���˶�����
$h-L=\frac{1}{2}g{{t}_{C}}^{2}$
xC=vCtC
��A��C�ɻ�е���غ㶨�ɵ�
$\frac{1}{2}m{{v}_{C}}^{2}=\frac{1}{2}m{{v}_{A}}^{2}+2mgL$
��xA=xC
����������ʽ���${{v}_{A}}^{2}=2g��h-L��$
С��Բ���˶�����ߵ�Aʱ${v}_{A}��\sqrt{gL}$
��h��$\frac{3}{2}$L
�𣺣�1��v����СֵΪ$\sqrt{gL}$����ʱ����С������F�Ĵ�СΪ�㣻
��2�����������С����׳����������ʱ��֮���tΪ$\frac{2\sqrt{3gL}}{g}$��
��3��O��������߶�h������L֮��Ӧ����Ĺ�ϵΪh��$\frac{3}{2}$L��
���� ������Բ���˶���ƽ���˶����ۺϣ�����ţ���˶����ɺͻ�е���غ��Ͻ����о�������ƽ���˶���Ҳ�������÷ֽ�ķ�����С������ٶȣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
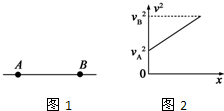 ��ͼ1��ʾ��ֱ��AB��ij�糡�е�һ���糡�ߣ�һ���ӽ��ڵ糡�������£��ɵ糡����A����ֱ���˶���B�㣬���ٶ�ƽ��v2��λ��x�Ĺ�ϵ��ͼ2��ʾ�������ж���ȷ���ǣ�������
��ͼ1��ʾ��ֱ��AB��ij�糡�е�һ���糡�ߣ�һ���ӽ��ڵ糡�������£��ɵ糡����A����ֱ���˶���B�㣬���ٶ�ƽ��v2��λ��x�Ĺ�ϵ��ͼ2��ʾ�������ж���ȷ���ǣ�������| A�� | A�㳡ǿС��B�㳡ǿ | |
| B�� | A��ĵ��Ƶ���B��ĵ��� | |
| C�� | ���Ӵ�A���˶���B�㣬�糡�������� | |
| D�� | ������A��ĵ�����С����B��ĵ����� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��

| A�� | L1������L2�䰵 | B�� | L1�䰵��L2���� | C�� | �͵������˶� | D�� | �͵������˶� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����

| A�� | a��b | B�� | b��a | C�� | b��c | D�� | d��b |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
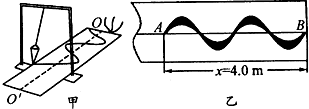 ͼ����ʾ����ʾ��ͼ���ɳ��ʵ��װ�ã�ɳ�ڿ���Ϊ�ڳ�L=1.0m�ĵ��ڣ���ڶ��ɿ�����г�˶���ʵ���У�ϸɳ�Ӱڶ��ŵ�©���ײ�����©������������ڶ�����ֱ�ķ�����������ֽ�壬©��ֽ���ϵ�ϸɳ�γ���ͼ����ʾ�Ĵ�ϸ�仯�й��ɵ�һ�����ߣ�
ͼ����ʾ����ʾ��ͼ���ɳ��ʵ��װ�ã�ɳ�ڿ���Ϊ�ڳ�L=1.0m�ĵ��ڣ���ڶ��ɿ�����г�˶���ʵ���У�ϸɳ�Ӱڶ��ŵ�©���ײ�����©������������ڶ�����ֱ�ķ�����������ֽ�壬©��ֽ���ϵ�ϸɳ�γ���ͼ����ʾ�Ĵ�ϸ�仯�й��ɵ�һ�����ߣ��鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ţ����Ϊ���Ǹı������˶�״̬��ԭ�� | |
| B�� | ����ʿ�����Ϊ����ά�������˶���ԭ�� | |
| C�� | �ѿ���ͨ��Ť��ʵ���һ�����������������G��ֵ | |
| D�� | ٤����ͨ��ʵ�鼰�������ƣ�ָ�����������˶���һ���ȱ���ֱ���˶� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ������ͼ��ʾ��·������һ����Դ���綯��ԼΪ9V�����費�ƣ��ĵ綯�ƺ�һ������Rx����ֵԼΪ2k������ȷֵ��ʵ���ҳ��˴����Դ�����ߺͿ����⣬��������һЩ���Ŀɹ�ѡ��
������ͼ��ʾ��·������һ����Դ���綯��ԼΪ9V�����費�ƣ��ĵ綯�ƺ�һ������Rx����ֵԼΪ2k������ȷֵ��ʵ���ҳ��˴����Դ�����ߺͿ����⣬��������һЩ���Ŀɹ�ѡ���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 �ҹ��Ķ��������Ѵ������Ƚ�ˮƽ�����{�������������ҹ���һ��һ·��ս�Թ�����ռ����Ҫһϯ����ν�����飬���ǰѴ������Ķ�������Ƕ���������Ԥ���IJ��������һ����ͼ��ʾ��ij���ζ�������2�ڶ���������6�ڷǶ����������Ӷ��ɣ�����������MΪ6.4��105kg��������ʻʱ���ڶ��������������ܹ���Ϊ4��107W�����趯�������ƽֱ·����ʻ���ܵ���������Ϊ������0.1����gȡ10m/s2����
�ҹ��Ķ��������Ѵ������Ƚ�ˮƽ�����{�������������ҹ���һ��һ·��ս�Թ�����ռ����Ҫһϯ����ν�����飬���ǰѴ������Ķ�������Ƕ���������Ԥ���IJ��������һ����ͼ��ʾ��ij���ζ�������2�ڶ���������6�ڷǶ����������Ӷ��ɣ�����������MΪ6.4��105kg��������ʻʱ���ڶ��������������ܹ���Ϊ4��107W�����趯�������ƽֱ·����ʻ���ܵ���������Ϊ������0.1����gȡ10m/s2�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | �������������4��105J | |
| B�� | �����Լ��ٶ�2m/s2�ȼ������������2��ĩʱ������ʵ�ʹ�����32kW | |
| C�� | �����Լ��ٶ�2m/s2�ȼ����������ﵽ����ٶ�ʱ��������Ϊ4��105J | |
| D�� | ���������ֶ�����������������ٶ�Ϊ5 m/sʱ������ٶ�Ϊ6m/s2 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com