
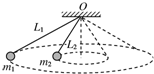
 如图所示,两根长度不同的细线分别系有两个小球m1、m2,细线的上端都系于O点.设法让两个小球在同一水平面上做匀速圆周运动.已知两细线长度之比L1:L2=$\sqrt{3}$:1,L1跟竖直方向的夹角为60°角,下列说法错误的是( )
如图所示,两根长度不同的细线分别系有两个小球m1、m2,细线的上端都系于O点.设法让两个小球在同一水平面上做匀速圆周运动.已知两细线长度之比L1:L2=$\sqrt{3}$:1,L1跟竖直方向的夹角为60°角,下列说法错误的是( )| A. | 两小球做匀速圆周运动的角速度相等 | |
| B. | 两小球做匀速圆周运动的线速度相等 | |
| C. | 两小球的质量比一定是m1:m2=$\sqrt{3}$:1 | |
| D. | L2细线跟竖直方向成45°角 |
分析 小球受重力和拉力,两个力的合力提供小球做圆周运动的向心力;通过合力提供向心力,比较出两球的角速度大小,从而比较出周期的关系;抓住小球距离顶点O的高度相同求出L2与竖直方向上的夹角;抓住小球距离顶点O的高度相同求出半径的关系,根据v=ωr比较线速度关系.
解答 解:A、设绳与竖直方向夹角为θ,水平面距悬点高为h,由牛顿第二定律得:
mgtanθ=mω2(h•tanθ)
则:ω=$\sqrt{\frac{g}{h}}$,由上式可知角速度与绳长无关,故A正确;
B、两球在同一水平面内做匀速圆周运动,则L1cos60°=L2cosθ,L1:L2=$\sqrt{3}$:1,解得θ=30°
由于v=ωr,故v正比于r,故线速度之比为:$\frac{{v}_{1}}{{v}_{2}}=\frac{h•tan60°}{h•tan30°}=\frac{3}{1}$;故BD错误;
C、根据mgtanθ=mLsinθω2,知小球做匀速圆周运动与质量无关,无法求出两小球的质量比,故C错误;
故选:A
点评 解决本题的关键会正确地受力分析,知道匀速圆周运动向心力是由物体所受的合力提供.


科目:高中物理 来源: 题型:选择题
 如图,在点电荷-q的电场中,放着一块带有一定电量、电荷均匀分布的绝缘矩形薄板,MN为其对称轴,O点为几何中心.点电荷-q与a、O、b之间的距离分别为d、2d、3d.已知图中a点的电场强度为零,则带电薄板在图中b点处产生的电场强度的大小和方向分别为( )
如图,在点电荷-q的电场中,放着一块带有一定电量、电荷均匀分布的绝缘矩形薄板,MN为其对称轴,O点为几何中心.点电荷-q与a、O、b之间的距离分别为d、2d、3d.已知图中a点的电场强度为零,则带电薄板在图中b点处产生的电场强度的大小和方向分别为( )| A. | $\frac{kq}{{d}^{2}}$,水平向右 | B. | $\frac{kq}{{d}^{2}}$,水平向左 | ||
| C. | $\frac{kq}{{d}^{2}}$+$\frac{kq}{9{d}^{2}}$,水平向右 | D. | $\frac{kq}{9{d}^{2}}$,水平向右 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
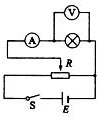 某小组做了一次”探究小灯泡额定电压”的实验.小灯泡上仅可读出标称功率0.55 W,别的数据完全模糊. 小组同学们先做了以下两项工作:
某小组做了一次”探究小灯泡额定电压”的实验.小灯泡上仅可读出标称功率0.55 W,别的数据完全模糊. 小组同学们先做了以下两项工作:| 次数 | 1 | 2 | 3 | 4 | 5 | 6 |
| U/V | 0.20 | 0.60 | 1.00 | 1.40 | 1.80 | 2.20 |
| 1/mA | 80 | 155 | 195 | 227 | 255 | 279 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
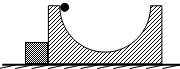 如图所示,光滑水平面上有半径R=15m的光滑半圆形凹槽,质量为2kg;凹槽左边紧挨着质量为3kg的物块.另有质量为10kg的小球从凹槽曲面左边的最高点无初速滑下,求小球能滑上凹槽右边的最大高度.
如图所示,光滑水平面上有半径R=15m的光滑半圆形凹槽,质量为2kg;凹槽左边紧挨着质量为3kg的物块.另有质量为10kg的小球从凹槽曲面左边的最高点无初速滑下,求小球能滑上凹槽右边的最大高度.查看答案和解析>>
科目:高中物理 来源: 题型:计算题
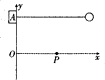 如图所示,在竖直平面的xOy坐标系内,一根长为l的不可伸长的细绳,一端固定在拉力传感器A上,另一端系一质量为m的小球.x轴上的P点固定一个表面光滑的小钉,P点与传感器A相距$\frac{3}{4}$l.现拉小球使细绳绷直并处在水平位置,然后由静止释放小球,当细绳碰到钉子后,小球可以绕钉子在竖直平面内做圆周运动.已知小球经过最低点时拉力传感器的示数为6mg,重力加速度大小为g,求:
如图所示,在竖直平面的xOy坐标系内,一根长为l的不可伸长的细绳,一端固定在拉力传感器A上,另一端系一质量为m的小球.x轴上的P点固定一个表面光滑的小钉,P点与传感器A相距$\frac{3}{4}$l.现拉小球使细绳绷直并处在水平位置,然后由静止释放小球,当细绳碰到钉子后,小球可以绕钉子在竖直平面内做圆周运动.已知小球经过最低点时拉力传感器的示数为6mg,重力加速度大小为g,求:查看答案和解析>>
科目:高中物理 来源: 题型:计算题
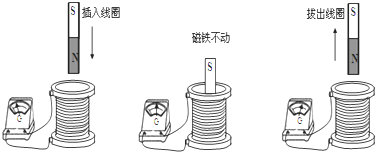
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
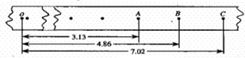 在《验证机械能守恒定律》的实验中:
在《验证机械能守恒定律》的实验中:查看答案和解析>>
科目:高中物理 来源: 题型:实验题
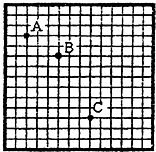 如图所示为一小球做平抛运动的闪光照相照片的一部分,图中背景方格的边长均为20cm.如果取g=10m/s2,那么:
如图所示为一小球做平抛运动的闪光照相照片的一部分,图中背景方格的边长均为20cm.如果取g=10m/s2,那么:查看答案和解析>>
科目:高中物理 来源: 题型:实验题
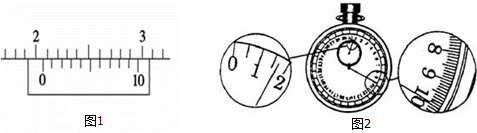
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com