
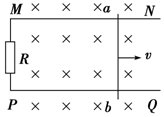
 ��ͼ��ʾ�������⻬�㹻����ƽ�н�������MN��PQˮƽ���ã����Ϊl=0.4m�����Ҷ˽���һ����ֵR=4���Ķ�ֵ���裬��������ĵ�����Բ��ƣ����˿�ܷ���ˮƽ���ϣ��ռ��д�ֱ���ƽ�����ǿ�ų����Ÿ�Ӧǿ��ΪB=1T��һ������r=1���Ľ���������F����������5m/s���ٶ��ڹ�������������˶�����
��ͼ��ʾ�������⻬�㹻����ƽ�н�������MN��PQˮƽ���ã����Ϊl=0.4m�����Ҷ˽���һ����ֵR=4���Ķ�ֵ���裬��������ĵ�����Բ��ƣ����˿�ܷ���ˮƽ���ϣ��ռ��д�ֱ���ƽ�����ǿ�ų����Ÿ�Ӧǿ��ΪB=1T��һ������r=1���Ľ���������F����������5m/s���ٶ��ڹ�������������˶��������� ��1������E=Blv����Ӧ�綯�ƣ��ٸ��ݱպϵ�·��ŷķ�������պϻ�·�еĸ�Ӧ������
��2������ŷķ�������ab�������Ʋ�Uab��
��3�����ݰ������ļ��㹫ʽ��ⰲ������С���ٸ��ݹ�������ƽ���������Ը�ʩ�ӵ�����F��
��� �⣺��1��������и�Ÿ���E=Blv=1��0.4��5V=2V
�ɱպϵ�·��ŷķ����֪I=$\frac{E}{R+r}=\frac{2}{4+1}A$=0.4A��
��2�������ֶ���֪��aΪ��Դ������bΪ��Դ����
����ŷķ���ɿɵã�Uab=IR�T0.4��4V=1.6V
��3������������ֱ���˶�����F=F��
��֪F��=BIl=1��0.4��0.4N=0.16N��
��������F=0.16N��
�𣺣�1����ʱ�պϻ�·�еĸ�Ӧ����Ϊ0.4A��
��2�����ڽ������˶�ab�������Ʋ�Ϊ1.6V��
��3��Ϊ���ָ������˶����Ը�ʩ�ӵ�����FΪ0.16N��
���� ���ڵ�Ÿ�Ӧ�����о�˼·������������һ�������ĽǶȣ��ص��Ƿ��������������µ������ƽ�����⣬����ƽ�������г����̣���һ���������������漰��Ÿ�Ӧ�����е�����ת�����⣬���ݶ��ܶ��������ܹ�ϵ���з�����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ����ͼ��ʾ��ʵ��װ�ù۲��ı�Ĥ��������ȼ�ƾ��Ʋ��ڵ�о����Щ�Σ�������һ�����Һ��Ĥ�Ľ���˿Ȧ������˵����ȷ���ǣ�������
����ͼ��ʾ��ʵ��װ�ù۲��ı�Ĥ��������ȼ�ƾ��Ʋ��ڵ�о����Щ�Σ�������һ�����Һ��Ĥ�Ľ���˿Ȧ������˵����ȷ���ǣ�������| A�� | ������˿Ȧ��ת30��ʱ��������ͬ������ת30�� | |
| B�� | ������˿Ȧ��ת45��ʱ��������ͬ������ת90�� | |
| C�� | ������˿Ȧ��ת60��ʱ��������ͬ������ת30�� | |
| D�� | �������Ʊ���ԭ��״̬���� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ��˹�ط����˵����Ĵ�ЧӦ������˵�Ÿ�Ӧ���� | |
| B�� | ��η����˵����Ĵ�ЧӦ�����о��ó����жϸ�Ӧ�����ķ���ķ���---��ζ��� | |
| C�� | ����������ЧӦʱ����Դ��Ƶ�ʱ仯�� | |
| D�� | ���������������ˡ����������������� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 �й��������2015��������˸߷��ĺ����ǣ������й��ŵ���ͬ������߷ֱ��ʶԵع۲����ǣ���ͼ��ʾ��A�Ǿ�ֹ�ڳ�����������ת�����壬B��C��ͬ�ڳ��ƽ���ڵ������������ǣ�Bλ����ظ߶ȵ��ڵ���뾶��Բ�ι���ϣ�C�Ǹ߷��ĺ����ǣ��������ж���ȷ���ǣ�������
�й��������2015��������˸߷��ĺ����ǣ������й��ŵ���ͬ������߷ֱ��ʶԵع۲����ǣ���ͼ��ʾ��A�Ǿ�ֹ�ڳ�����������ת�����壬B��C��ͬ�ڳ��ƽ���ڵ������������ǣ�Bλ����ظ߶ȵ��ڵ���뾶��Բ�ι���ϣ�C�Ǹ߷��ĺ����ǣ��������ж���ȷ���ǣ�������| A�� | ����A�������ת�Ľ��ٶȴ�������B�Ľ��ٶ� | |
| B�� | ����B�����ٶ�С������C�����ٶ� | |
| C�� | ����A�������ת�����ڴ�������C������ | |
| D�� | ����A�������ת�����ļ��ٶ�С������C�����ļ��ٶ� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
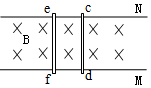 ��ͼ��M��N��������ͬһˮƽ�����ֻ���ƽ�еĹ⻬�������죬ef��cdΪ����������������װ�÷�����ǿ�ų��У����ef�������������ص��������˶�����ͨ��cd�ĵ��������Լ�cd���˶������ǣ�������
��ͼ��M��N��������ͬһˮƽ�����ֻ���ƽ�еĹ⻬�������죬ef��cdΪ����������������װ�÷�����ǿ�ų��У����ef�������������ص��������˶�����ͨ��cd�ĵ��������Լ�cd���˶������ǣ�������| A�� | c��d������ | B�� | d��c������ | C�� | c��d������ | D�� | d��c������ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
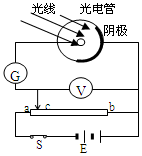 ����ͼ��ʾ��װ���о����ЧӦ�������ù�������Ϊ2.75eV�����䵽������ʱ�����˹��ЧӦ��������G��ʾ����Ϊ�㣻�ƶ��������Ĵ���c�����ֵ���ѹ����ʾ�����ڻ����1.7Vʱ��������ʾ��Ϊ0��������˵����ȷ���ǣ�������
����ͼ��ʾ��װ���о����ЧӦ�������ù�������Ϊ2.75eV�����䵽������ʱ�����˹��ЧӦ��������G��ʾ����Ϊ�㣻�ƶ��������Ĵ���c�����ֵ���ѹ����ʾ�����ڻ����1.7Vʱ��������ʾ��Ϊ0��������˵����ȷ���ǣ�������| A�� | ����ӵ���������ʼ��Ϊ1.05eV | |
| B�� | �����������ݳ���Ϊ1.05eV | |
| C�� | ���S�Ͽ�������G���е������� | |
| D�� | ��������Ϊ2.5eV�Ĺ������䣬�ƶ��������Ĵ���c��������G��Ҳ�����е��� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 ��ͼ��ʾ��һ����С��������ƽ�а�������ڲ����պϵ��S������������ϸ������ֱ����н�Ϊ����������˵����ȷ���ǣ�������
��ͼ��ʾ��һ����С��������ƽ�а�������ڲ����պϵ��S������������ϸ������ֱ����н�Ϊ����������˵����ȷ���ǣ�������| A�� | ���ֵ��S�պϣ�ʹ�������Կ���һЩ���������� | |
| B�� | ���ֵ��S�պϣ���������������Ƭ�����ƶ����������� | |
| C�� | �Ͽ����S��ʹ�������Կ���һЩ��������С | |
| D�� | �Ͽ����S������ϸ���նϣ�С���������˶� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����

| A�� | $\frac{{u}_{2}-{u}_{1}}{nB{L}_{2}��{t}_{2}-{t}_{1}��}$ $\frac{{u}_{2}+{u}_{1}}{2nB{L}_{2}}$��t2-t1�� | |
| B�� | $\frac{{u}_{2}+{u}_{1}}{nB{L}_{2}��{t}_{2}-{t}_{1}��}$ $\frac{{u}_{2}+{u}_{1}}{2nB{L}_{2}}$��t2-t1�� | |
| C�� | $\frac{{u}_{2}+{u}_{1}}{nB{L}_{2}��{t}_{2}-{t}_{1}��}$ $\frac{{u}_{2}+{u}_{1}}{2nB{L}_{2}}$��t2-t1�� | |
| D�� | $\frac{{u}_{2}-{u}_{1}}{nB{L}_{2}��{t}_{2}-{t}_{1}��}$ $\frac{{u}_{2}+{u}_{1}}{2nB{L}_{2}}$��t2+t1�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com