
| A. | 冥王星的卫星查龙(charon)绕其运转的线速度和轨道半径 | |
| B. | 冥王星的卫星查龙(charon)绕其运转的周期和轨道半径 | |
| C. | 冥王星绕太阳运转的周期和轨道半径 | |
| D. | 冥王星绕太阳运转的线速度和轨道半径 |
分析 研究卫星绕行星做匀速圆周运动,根据万有引力提供向心力,列出等式只能求出中心体的质量.
解答 解:A、冥王星的卫星查龙(charon)围绕冥王星做圆周运动,根据万有引力提供向心力,列出等式:
$G\frac{Mm}{{r}_{\;}^{2}}=m\frac{{v}_{\;}^{2}}{r}$,得$M=\frac{{v}_{\;}^{2}r}{G}$,v为卫星查龙线速度,r为卫星查龙的轨道半径,故A正确.
B、冥王星的卫星查龙(charon)围绕冥王星做圆周运动,根据万有引力提供向心力,列出等式:
$G\frac{Mm}{{r}_{\;}^{2}}=m\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}r$,得$M=\frac{4{π}_{\;}^{2}{r}_{\;}^{3}}{G{T}_{\;}^{2}}$,T为卫星查龙周期,r为卫星查龙的轨道半径,故B正确;
CD、根据万有引力提供向心力,列出等式只能求出中心体的质量,只能求出中心天体的质量,故CD错误;
故选:AB
点评 本题考查万有引力定律在天体中的应用,解题的关键掌握万有引力提供向心力,只能求出中心天体的质量,而不能求出环绕天体的质量.


 名校课堂系列答案
名校课堂系列答案科目:高中物理 来源: 题型:多选题
| A. | 当m1和m2之间的距离趋近于零时,F趋于无穷大 | |
| B. | 只要m1和m2是球体,就可用上式求解万有引力 | |
| C. | 只有m1和m2看成质点时,才可用上式求m1和m2间的万有引力 | |
| D. | 任何两个物体都存在万有引力 |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题

查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 质点的速度每经1s增加2m/s | |
| B. | 质点的加速度越来越大 | |
| C. | 质点任1s内的平均速度比前1s内的平均速度大2m/s | |
| D. | 质点在任1s内位移比前1s内位移大2m |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 受连日暴雨影响,2016 年5 月8 日上午,抚州市黎川县发生内涝及泥石流等地质灾害.从当地消防部门获悉,截止8 日下午已经营救出被困群众40 余人,救援工作仍在进行.假设一块质量为2kg的石块随着雨水由静止开始沿倾角为30°、长50m 的斜坡滑下,则石块下落至坡底时(忽略一切阻力,取g=10m/s2)( )
受连日暴雨影响,2016 年5 月8 日上午,抚州市黎川县发生内涝及泥石流等地质灾害.从当地消防部门获悉,截止8 日下午已经营救出被困群众40 余人,救援工作仍在进行.假设一块质量为2kg的石块随着雨水由静止开始沿倾角为30°、长50m 的斜坡滑下,则石块下落至坡底时(忽略一切阻力,取g=10m/s2)( )| A. | 石块具有的动能为1000J | B. | 石块具有的动能为500J | ||
| C. | 重力的瞬时功率为200W | D. | 重力的瞬时功率为100$\sqrt{5}$W |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 一组宇航员乘坐太空穿梭机S,去修理位于离地球表面h=6.0×105m的圆形轨道上的太空望远镜H.机组人员使穿梭机S进入与H相同的轨道并关闭助推火箭,望远镜则在穿梭机前方数千米处,如图所示.已知地球半径为R=6.4×106m,地球表面重力加速度为g=9.8m/s2,第一宇宙速度为v=7.9km/s.
一组宇航员乘坐太空穿梭机S,去修理位于离地球表面h=6.0×105m的圆形轨道上的太空望远镜H.机组人员使穿梭机S进入与H相同的轨道并关闭助推火箭,望远镜则在穿梭机前方数千米处,如图所示.已知地球半径为R=6.4×106m,地球表面重力加速度为g=9.8m/s2,第一宇宙速度为v=7.9km/s.查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
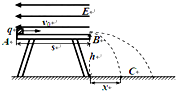 如图所示,绝缘的光滑水平桌面高为h=1.25m、长为s=2m,桌面上方有一个水平向左的匀强电场.一个质量为m=2×10-3kg、带电量为q=+5.0×10-8C的小物体自桌面的左端A点以初速度vA=6m/s向右滑行,离开桌子边缘B后,落在水平地面上C点.C点与B点的水平距离x=1m,不计空气阻力,取g=10m/s2.
如图所示,绝缘的光滑水平桌面高为h=1.25m、长为s=2m,桌面上方有一个水平向左的匀强电场.一个质量为m=2×10-3kg、带电量为q=+5.0×10-8C的小物体自桌面的左端A点以初速度vA=6m/s向右滑行,离开桌子边缘B后,落在水平地面上C点.C点与B点的水平距离x=1m,不计空气阻力,取g=10m/s2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com