
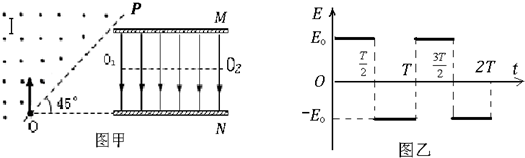
分析 (1)求出粒子轨道半径,应用牛顿第二定律可以求出粒子a、b从I磁场边界射出时的速度va、vb.
(2)求出粒子在磁场中、在电场中、在电磁场外的运动时间,然后求出总运动时间.
(3)作出粒子在电场中的运动轨迹,应用类平抛运动规律分析答题.
解答 解:(1)如图所示,粒子a、b在磁场中均速转过90°,平行于金属板进入电场.
由几何关系可得:${r}_{a}=\frac{1}{2}d$,rb=d…①
由牛顿第二定律可得
$q{v}_{a}B=\frac{m{v}_{a}^{2}}{{r}_{a}}$ …②
$q{v}_{b}B=\frac{m{v}_{b}^{2}}{{r}_{b}}$ …③
解得:${v}_{a}=\frac{qBd}{2m}$,${v}_{b}=\frac{qBd}{m}$
(2)粒子a在磁场中运动轨迹如图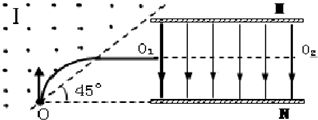
在磁场中运动周期为:${T}_{0}=\frac{2πm}{qB}$ …④
在磁场中运动时间:${t}_{1}=\frac{{T}_{0}}{4}=\frac{πm}{2qB}$ …⑤
粒子在电磁场边界之间运动时,水平方向做匀速直线运动,所用时间为
${t}_{2}=\frac{(\frac{d}{2}+L)}{{v}_{a}}$ …⑥
由 ④⑤⑥则全程所用时间为:$t={t}_{1}+{t}_{2}=\frac{πm}{2qB}+\frac{m(d+2L)}{qBd}$
(3)粒子在磁场中运动的时间相同,a、b同时离开Ⅰ磁场,a比b进入电场落后时间$△t=\frac{d}{2{v}_{a}}=\frac{m}{qB}=\frac{T}{4}$ …⑦
故粒子b在t=0时刻进入电场.
由于粒子a在电场中从O2射出,在电场中竖直方向位移为0,故a在板间运动的时间ta是周期的整数倍,由于vb=2va,b在电场中运动的时间是tb=$\frac{1}{2}$ta,可见b在电场中运动的时间是半个周期的整数倍即${t}_{b}=\frac{L}{{v}_{b}}=n•\frac{T}{2}$ …⑧
$n=\frac{2L}{Tv}$ …⑨
粒子b在$\frac{T}{2}$内竖直方向的位移为$y=\frac{1}{2}a(\frac{T}{2})^{2}$ …⑩
粒子在电场中的加速度$a=\frac{q{E}_{0}}{m}$
由题知$T=\frac{4m}{qB}$
粒子b能穿出板间电场应满足ny≤d
解得${E}_{0}≤\frac{q{d}^{2}{B}^{2}}{mL}$
答:(1)粒子a、b从磁场边界射出时的速度va、vb分别是:$\frac{qBd}{2m}$和$\frac{qBd}{m}$;
(2)粒子a从O点进入磁场到射出O2点运动的总时间是$\frac{πm}{2qB}+\frac{m(d+2L)}{qBd}$;
(3)如果交变电场的周期T=$\frac{4m}{qB}$,要使粒子b能够穿出板间电场,则电场强度大小E0满足的条件${E}_{0}≤\frac{q{d}^{2}{B}^{2}}{mL}$.
点评 本题考查了带电粒子在电场与磁场中的运动,分析清楚粒子运动过程、作出粒子运动轨迹是正确解题的关键,应用牛顿第二定律、粒子在磁场中做匀速圆周运动的周期公式、牛顿第二定律、运动学公式即可正确解题.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中物理 来源: 题型:选择题
| A. | 物体速度变化越大,加速度越大 | B. | 物体速度变化越快,加速度越大 | ||
| C. | 物体位置变化越大,加速度越大 | D. | 物体位置变化越快,加速度越大 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
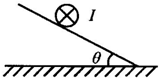 如图所示,在倾角为θ的光滑斜面上,放置一质量为m的导体棒,棒长为l,棒中通有垂直纸面向里的电流,电流大小为I.若使金属棒静止在斜面上,则下面关于磁感 应强度B的判断正确的是( )
如图所示,在倾角为θ的光滑斜面上,放置一质量为m的导体棒,棒长为l,棒中通有垂直纸面向里的电流,电流大小为I.若使金属棒静止在斜面上,则下面关于磁感 应强度B的判断正确的是( )| A. | B的方向垂直斜面向上,B=$\frac{mgsinθ}{IL}$,B为最小值 | |
| B. | B的方向平行斜面向上,B=$\frac{mgsinθ}{IL}$,B为最小值 | |
| C. | B的方向竖直向上,B=$\frac{mg}{IL}$,此时金属棒对导轨无压力 | |
| D. | B的方向水平向左,B=$\frac{mg}{IL}$,此时金属棒对导轨无压力 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
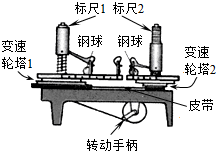 用如图所示的装置来探究小球做圆周运动所需向心力的大小F与质量m、角速度ω和半径r之间的关系.两个变速轮塔通过皮带连接,转动手柄使长槽和短槽分别随变速轮塔匀速转动,槽内的钢球就做匀速圆周运动.横臂的挡板对钢球的压力提供向心力,钢球对挡板的反作用力通过横臂的杠杆作用使弹簧测力筒下降,从而露出标尺,标尺上的红白相间的等分格显示出两个钢球所受向心力的比值.
用如图所示的装置来探究小球做圆周运动所需向心力的大小F与质量m、角速度ω和半径r之间的关系.两个变速轮塔通过皮带连接,转动手柄使长槽和短槽分别随变速轮塔匀速转动,槽内的钢球就做匀速圆周运动.横臂的挡板对钢球的压力提供向心力,钢球对挡板的反作用力通过横臂的杠杆作用使弹簧测力筒下降,从而露出标尺,标尺上的红白相间的等分格显示出两个钢球所受向心力的比值.查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,一轻质弹簧下端固定在粗糙的斜面底端的档板上,弹簧上端处于自由状态,斜面倾角为θ,一质量为m的物块(可视为质点)从离弹簧上端距离为L1处由静止释放,物块与斜面间动摩擦因数为?,物块在整个过程中的最大速度为v,弹簧被压缩到最短时物体离释放点的距离为L2 (重力加速度为g).则( )
如图所示,一轻质弹簧下端固定在粗糙的斜面底端的档板上,弹簧上端处于自由状态,斜面倾角为θ,一质量为m的物块(可视为质点)从离弹簧上端距离为L1处由静止释放,物块与斜面间动摩擦因数为?,物块在整个过程中的最大速度为v,弹簧被压缩到最短时物体离释放点的距离为L2 (重力加速度为g).则( )| A. | 从物块释放到弹簧被压缩到最短的过程中,系统损失的机械能为?mgL2cosθ | |
| B. | 从物块释放到弹簧压缩到最短的过程中,物体重力势能的减少量等于弹簧弹性势能的增加量与系统产生的内能之和 | |
| C. | 物块的速度最大时,弹簧的弹性势能为mgL1(sinθ-?cosθ)-$\frac{1}{2}$mv2 | |
| D. | 物块的最大动能为mgL1(sinθ-?cosθ) |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
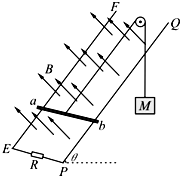 如图所示,无限长金属导轨EF、PQ固定在倾角为θ=53°的光滑绝缘斜面上,轨道间距L=1m,底部接入一阻值为R=0.4Ω的定值电阻,上端开口.垂直斜面向上的匀强磁场的磁感应强度B=2T.一质量为m=0.5kg的金属棒ab与导轨接触良好,ab与导轨间动摩擦因数μ=0.2,ab连入导轨间的电阻r=0.1Ω,电路中其余电阻不计.现用一质量为M=2.86kg的物体通过一不可伸长的轻质细绳绕过光滑的定滑轮与ab相连.由静止释放M,当M下落高度h=2.0m时,ab开始匀速运动(运动中ab始终垂直导轨,并接触良好).不计空气阻力,sin53°=0.8,cos53°=0.6,取g=10m/s2.求:
如图所示,无限长金属导轨EF、PQ固定在倾角为θ=53°的光滑绝缘斜面上,轨道间距L=1m,底部接入一阻值为R=0.4Ω的定值电阻,上端开口.垂直斜面向上的匀强磁场的磁感应强度B=2T.一质量为m=0.5kg的金属棒ab与导轨接触良好,ab与导轨间动摩擦因数μ=0.2,ab连入导轨间的电阻r=0.1Ω,电路中其余电阻不计.现用一质量为M=2.86kg的物体通过一不可伸长的轻质细绳绕过光滑的定滑轮与ab相连.由静止释放M,当M下落高度h=2.0m时,ab开始匀速运动(运动中ab始终垂直导轨,并接触良好).不计空气阻力,sin53°=0.8,cos53°=0.6,取g=10m/s2.求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
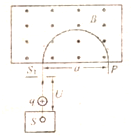 质谱仪是一种带电粒子质量和分析同位素的重要工具,它的构造原理如图所示,粒子源S产生电荷量q的某种正离子,粒子产生时的速度很小,可以看作是静止的,离子经过电压U加速后形成离子电流,然后垂直于磁场方向进入磁感应强度为B的入口处S1的距离为a,粒子流的电流为1,请回答下列问题:
质谱仪是一种带电粒子质量和分析同位素的重要工具,它的构造原理如图所示,粒子源S产生电荷量q的某种正离子,粒子产生时的速度很小,可以看作是静止的,离子经过电压U加速后形成离子电流,然后垂直于磁场方向进入磁感应强度为B的入口处S1的距离为a,粒子流的电流为1,请回答下列问题:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 若能观测到该行星的轨道半径,可求出该行星所受的万有引力 | |
| B. | 若已知该行星的密度和半径,可求出该行星的轨道半径 | |
| C. | 根据地球的公转周期与轨道半径,可求出该行星的轨道半径 | |
| D. | 若该行星的密度与地球的密度相等,可求出该行星表面的重力加速度 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com