
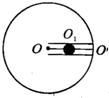
 ��ͼ��ʾ����ˮƽ Բ������һ��Բ�ĵĹ⻬С�ۣ�����������ԭ��������ϵ������ͬ����Ƥ����סһ����Ϊm��С��һ����Ƥ��˩��O�㣬��һ��˩��O��㣬����OΪԲ�̵����ģ�O�����Բ�̵ı�Ե�ϣ���Ƥ���ľ���ϵ��Ϊk��ԭ��ΪԲ�̰뾶R��$\frac{1}{3}$����ʹԲ�̽��ٶ����㻺������������
��ͼ��ʾ����ˮƽ Բ������һ��Բ�ĵĹ⻬С�ۣ�����������ԭ��������ϵ������ͬ����Ƥ����סһ����Ϊm��С��һ����Ƥ��˩��O�㣬��һ��˩��O��㣬����OΪԲ�̵����ģ�O�����Բ�̵ı�Ե�ϣ���Ƥ���ľ���ϵ��Ϊk��ԭ��ΪԲ�̰뾶R��$\frac{1}{3}$����ʹԲ�̽��ٶ����㻺������������| A�� | ��=$\sqrt{\frac{k}{2m}}$ʱ��OO�����Ƥ������ԭ�� | B�� | ��=$\sqrt{\frac{k}{5m}}$ʱ��С���Բ�ľ���Ϊ$\frac{5R}{9}$ | ||
| C�� | ��=$\sqrt{\frac{3k}{5m}}$ʱ��С���Բ�ĵľ���Ϊ$\frac{5}{6}$R | D�� | ��=$\sqrt{\frac{3k}{5m}}$ʱ��OO1����Ƥ���ĵ���ΪkR |
���� �����Ƥ��������ʱ�����ڲ����������ṩ�����������ţ�ٵڶ����ɺͺ��˶������Բ��ת���Ľ��ٶȴ�С�������ٶ�С�ڴ�ʱ���ٶ�ʱ������Ƥ������������������������ʽ��Ϻ��˶������С���Բ�ľ��룬�����ٶȴ��ڴ�ʱ���ٶ�ʱ���Ҳ���Ƥ����������������������ʽ��Ϻ��˶�����⼴�ɣ�
��� �⣺A����Բ�̵Ľ��ٶ�Ϊ��0ʱ�������Ƥ��ǡ����������
����$k��\frac{2}{3}R-\frac{1}{3}R��=m\frac{2}{3}R{{��}_{0}}^{2}$��
�ɵ�${��}_{0}=\sqrt{\frac{k}{2m}}$����A��ȷ��
B��$\sqrt{\frac{k}{5m}}��\sqrt{\frac{k}{2m}}$��������Ƥ������������
���ʱ�뾶Ϊr1�����У�$k��{r}_{1}-\frac{1}{3}R��-k��R-{r}_{1}-\frac{1}{3}R��=m{r}_{1}{��}^{2}$
��ã�${r}_{1}=\frac{5R}{9}$����B��ȷ��
C����=$\sqrt{\frac{3k}{5m}}$$��\sqrt{\frac{k}{2m}}$�����Ҳ���Ƥ����������
���ʱ�뾶Ϊr2�����У�
$k��{r}_{2}-\frac{1}{3}R��=m{r}_{2}{��}^{2}$��
���${r}_{2}=\frac{5}{6}R$��
��ʱOO1����Ƥ���ĵ���ΪF=$k��{r}_{2}-\frac{1}{3}R��=\frac{1}{2}kR$����C��ȷ��D����
��ѡ��ABC
���� �������Ĺؼ�֪��Բ���˶�����������Դ�����ţ�ٵڶ����ɺͺ��˶����ۺ���⣬�Ѷ��еȣ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�������

�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | 5��2 | B�� | 5��4 | C�� | 25��6 | D�� | 25��12 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
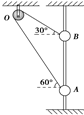 ��ͼ��ʾ��һ������ϸ�������������������С��A��B�����Ƕ�����һ���⻬����ֱ���ϣ�����ϸ���뻬��֮���Ħ����������ƽ��ʱOA����ˮƽ����ļн�Ϊ60�㣬OB����ˮƽ����ļн�Ϊ30�㣬��˶�A��B�ĵ���֮��Ϊ��������
��ͼ��ʾ��һ������ϸ�������������������С��A��B�����Ƕ�����һ���⻬����ֱ���ϣ�����ϸ���뻬��֮���Ħ����������ƽ��ʱOA����ˮƽ����ļн�Ϊ60�㣬OB����ˮƽ����ļн�Ϊ30�㣬��˶�A��B�ĵ���֮��Ϊ��������| A�� | $\frac{{N}_{A}}{{N}_{B}}=\frac{\sqrt{3}}{1}$ | B�� | $\frac{{N}_{A}}{{N}_{B}}=\frac{\sqrt{3}}{3}$ | C�� | $\frac{{N}_{A}}{{N}_{B}}=\frac{\sqrt{3}}{2}$ | D�� | $\frac{{N}_{A}}{{N}_{B}}=\frac{2}{\sqrt{3}}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������

�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ������ | B�� | ��˹�� | C�� | ���� | D�� | ���˹Τ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 �������ҹ�������·��չѸ�٣�����֪ij����������������Ϊm����ͼ��֪��������ΪL�������߶Ȳ�Ϊh���������ٶ�Ϊg���������Ҫ����뾶ΪR����������ʣ��������������ٶ���Ϊ���˵��ǣ�������
�������ҹ�������·��չѸ�٣�����֪ij����������������Ϊm����ͼ��֪��������ΪL�������߶Ȳ�Ϊh���������ٶ�Ϊg���������Ҫ����뾶ΪR����������ʣ��������������ٶ���Ϊ���˵��ǣ�������| A�� | $\sqrt{\frac{gRh}{\sqrt{{L}^{2}-{h}^{2}}}}$ | B�� | $\sqrt{\frac{gRh}{\sqrt{{L}^{2}-{R}^{2}}}}$ | C�� | $\sqrt{\frac{gR\sqrt{{L}^{2}-{h}^{2}}}{h}}$ | D�� | $\sqrt{\frac{gRL}{h}}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ��ʾ��ˮƽ�⻬��������һ����M=2kg�ij�ľ�壬�ڳ�ľ�������һ����Ϊm=1kg��С��飬С�����ľ���Ķ�Ħ������Ϊ��=0.4��һ��ʼ��С�����ľ�嶼���ھ�ֹ״̬���ֶ����ʩ��F=12N�ĺ�����3s��ȥ�ú�����ҪʹС��鲻�ӳ�ľ���ϻ���������ľ�������ж��
��ͼ��ʾ��ˮƽ�⻬��������һ����M=2kg�ij�ľ�壬�ڳ�ľ�������һ����Ϊm=1kg��С��飬С�����ľ���Ķ�Ħ������Ϊ��=0.4��һ��ʼ��С�����ľ�嶼���ھ�ֹ״̬���ֶ����ʩ��F=12N�ĺ�����3s��ȥ�ú�����ҪʹС��鲻�ӳ�ľ���ϻ���������ľ�������ж���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com