
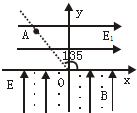
 如图所示,虚线AO与沿水平方向的x轴的夹角为135°,x轴上、下方分别有如图所示的水平向右的匀强电场E1和竖直向上的匀强电场E2,且电场强度E1=E2=20N/C,x轴下方还存在垂直于纸面向外的匀强磁场B,已知磁感应强度B=20T.现将一个带正电微粒从虚线AO上的A点由静止释放,微粒恰能沿AO做直线运动.A点离原点O的距离d=$\frac{\sqrt{2}}{10}$m,重力加速度g取10m/s2.求:
如图所示,虚线AO与沿水平方向的x轴的夹角为135°,x轴上、下方分别有如图所示的水平向右的匀强电场E1和竖直向上的匀强电场E2,且电场强度E1=E2=20N/C,x轴下方还存在垂直于纸面向外的匀强磁场B,已知磁感应强度B=20T.现将一个带正电微粒从虚线AO上的A点由静止释放,微粒恰能沿AO做直线运动.A点离原点O的距离d=$\frac{\sqrt{2}}{10}$m,重力加速度g取10m/s2.求:分析 (1)由牛顿第二定律求出尘粒的加速度,由速度位移公式求出速度.尘粒在匀强磁场中做匀速圆周运动,牛顿第二定律与周期公式求出尘粒的运动时间.
(2)尘粒离开磁场后做类平抛运动,由类平抛运动规律可以求出距离L.
解答 解:(1)由题意,在x轴上方的电场中,微粒受电场力和重力的作用,将沿AO作初速为零的匀加速直线运动.设微粒质量为m、电荷量为q,到达O点的速度为v,则有 qE=mg,即$\frac{m}{q}=\frac{E}{g}=2kg/C$
合力${F}_{合}=\frac{mg}{cos45°}$
加速度为:$a=\frac{{F}_{合}}{m}=\frac{g}{cos45°}=10\sqrt{2}m/{s}^{2}$
由v2=2ad,
代入数据解得:v=2m/s
在x轴下方的复合场中,因微粒所受的重力和电场力平衡,故微粒将在洛伦兹力的作用下做匀速圆周运动.其周期为:
$T=\frac{2πm}{qB}$
代入数据得:T=0.628s
依题意作出微粒在磁场中运动的轨迹示意图(如图),可知微粒从进入磁场区域直到离开,所用时间为:
$t=\frac{3}{4}T=\frac{3}{4}×0.628s=0.471$s
(2)微粒在磁场中做圆周运动的半径:$R=\frac{mv}{qB}$
代入数据得:R=0.2m
微粒离开磁场重新进入x轴上方的电场中,速度方向与x轴成45°,沿速度方向的分运动为匀速直线运动,垂直速度方向(即AO方向)的分运动为初速度为零的匀加速直线运动.
沿速度方向有s1=R=vt′,$t′=\frac{R}{v}=\frac{0.2}{2}s=0.1$s
垂直速度方向有:${s}_{2}=\frac{1}{2}at{′}^{2}$
代入数据得:${s}_{2}=\frac{\sqrt{2}}{20}$m
因s2<R,故微粒一定在x轴上方穿越AO直线,所以微粒第一次回到AO直线上的位置Q时,离原点O的距离为$L=R-{s}_{2}=0.2-\frac{\sqrt{2}}{20}≈0.13$m
答:(1)微粒从进入磁场区域开始到离开磁场区域所经历的时间是0.471s;
(2)微粒第一次回到OA直线上的某位置时,离原点O的距离是0.13m.
点评 本题考查了带电尘粒在电场与磁场中的运动,分析清楚运动过程是正确解题的前提与关键,分析清楚运动过程后,应用牛顿第二定律、运动学公式、类平抛运动规律即可正确解题.


 阅读快车系列答案
阅读快车系列答案科目:高中物理 来源: 题型:填空题
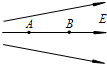 如图所示,A、B是电场中的两个点,由图可知电场强度EA>EB(填“>”或“<”).将一点电荷先后放在A、B两点,它所受的电场力大小FA>FB(填“>”或“<”),将一正点电荷从A点移动到B点,电场力做正功(选填“正功”或“负功”).
如图所示,A、B是电场中的两个点,由图可知电场强度EA>EB(填“>”或“<”).将一点电荷先后放在A、B两点,它所受的电场力大小FA>FB(填“>”或“<”),将一正点电荷从A点移动到B点,电场力做正功(选填“正功”或“负功”).查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 物体间不接触也能产生弹力 | |
| B. | 只要两物体接触就必定有弹力 | |
| C. | 只有弹簧才能产生弹力 | |
| D. | 弹力是发生弹性形变的物体,由于要恢复原状,对与它接触的物体产生的力 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 5N | B. | 8N | C. | 12N | D. | 15N |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 公式R=ρ$\frac{L}{S}$ C=$\frac{εS}{4πKd}$是R和C的决定式 | |
| B. | 公式I=$\frac{U}{R}$,E=$\frac{F}{q}$,R=$\frac{U}{I}$ B=$\frac{F}{IL}$ C=$\frac{Q}{U}$ a=$\frac{△v}{△t}$ 中的I、E、R、B、C、a等这些物理量的大小都是由各自公式中的物理量大小决定的 | |
| C. | 由万有引力公式和静电力公式知,其中的万有引力常量和静电力常量都是没有单位的常数 | |
| D. | 由公式F=ma知,一定质量的物体所受合外力由运动加速度a决定 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 一列简谐横波图象如图所示,t1时刻的波形如图中实线所示,t2时刻的波形如图中虚线所示,已知△t=t2-t1=0.5s,求:
一列简谐横波图象如图所示,t1时刻的波形如图中实线所示,t2时刻的波形如图中虚线所示,已知△t=t2-t1=0.5s,求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
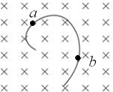 一带电粒子沿垂直于磁场的方向射入一匀强磁场.粒子的一段径迹如图.径迹上的每一小段都可近似看成圆弧.由于带电粒子使沿途的空气电离,粒子的能量逐渐减小(带电量不变).从图可以确定( )
一带电粒子沿垂直于磁场的方向射入一匀强磁场.粒子的一段径迹如图.径迹上的每一小段都可近似看成圆弧.由于带电粒子使沿途的空气电离,粒子的能量逐渐减小(带电量不变).从图可以确定( )| A. | 粒子带正电,从a运动到b | B. | 粒子带正电,从b运动到a | ||
| C. | 粒子带负电,从a运动到b | D. | 粒子带负电,从b到运动a |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
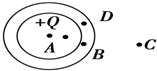 如图所示,球壳内部球心位置放置正点电荷Q,球壳内A点,壳壁中B点、D点,壳外C点,则下列说法不正确的是( )
如图所示,球壳内部球心位置放置正点电荷Q,球壳内A点,壳壁中B点、D点,壳外C点,则下列说法不正确的是( )| A. | B、D两点的电势相等 | |
| B. | A、C两点的电势相等 | |
| C. | 如果球壳外部接地,B、D两点的电势等于零 | |
| D. | φA>φB=φD>φC |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com