
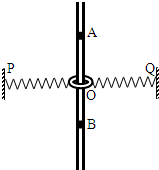
 ��ͼ��ʾ��һ������Ϊm�ĸ���Բ�����ڴֲڵ���ֱ�̶�ϸ���ϣ�Բ����ֱ���Դ���ϸ�˵�ֱ����Բ����������������ͬ�����ʵ��ɵ�һ�����������ʵ��ɵ���һ�����ں�Բ��ͬһ�߶ȵ�ǽ���ϵ�P��Q���㴦�����ɵľ���ϵ��Ϊk�����Բ������O�㣬���ɴ���ԭ��״̬�ҵ��ɵ�ԭ��ΪL��ϸ�������A��B���㵽O��ľ��붼ΪL����Բ������A���ɾ�ֹ�ͷţ��������ٶ�Ϊg������Բ����A���˶���B��Ĺ��̣�����˵����ȷ���ǣ�������
��ͼ��ʾ��һ������Ϊm�ĸ���Բ�����ڴֲڵ���ֱ�̶�ϸ���ϣ�Բ����ֱ���Դ���ϸ�˵�ֱ����Բ����������������ͬ�����ʵ��ɵ�һ�����������ʵ��ɵ���һ�����ں�Բ��ͬһ�߶ȵ�ǽ���ϵ�P��Q���㴦�����ɵľ���ϵ��Ϊk�����Բ������O�㣬���ɴ���ԭ��״̬�ҵ��ɵ�ԭ��ΪL��ϸ�������A��B���㵽O��ľ��붼ΪL����Բ������A���ɾ�ֹ�ͷţ��������ٶ�Ϊg������Բ����A���˶���B��Ĺ��̣�����˵����ȷ���ǣ�������| A�� | Բ��ͨ��O��ļ��ٶ�С��g | |
| B�� | Բ����O����ٶ���� | |
| C�� | Բ����A��ʱ�ļ��ٶȴ�СΪg+$\frac{��2-\sqrt{2}��kL}{m}$ | |
| D�� | Բ����B����ٶ�Ϊ2$\sqrt{gL}$ |
���� ��Բ��Ϊ�о�����Բ���ڳ�ʼλ���ٶ�Ϊ0����A�㵽B���˶������У����ɵ��α����ȼ�С�����ӣ���������ֱ����ļн������Ӻ��С��ͨ��O��ʱ���ٶȺͼ��ٶȣ�ͨ���������������������ţ�ٵڶ����ɿ������Բ����A��ļ��ٶȣ����ݹ��ܹ�ϵ���Է���Բ����B����ٶȣ�
���  �⣺A��Բ��ͨ��O��ʱ��ˮƽ�������Ϊ�㣬��ֱ����ֻ���������ʼ��ٶȵ���g����A����
�⣺A��Բ��ͨ��O��ʱ��ˮƽ�������Ϊ�㣬��ֱ����ֻ���������ʼ��ٶȵ���g����A����
B��Բ������ƽ��ʱ�ٶ����Ӧ��O���·�����B����
C��Բ�����»���������ֲ�ϸ��֮����ѹ��������Ħ��������A���Բ����������������ͼ�����ݼ��ι�ϵ����A�㵯���쳤$��\sqrt{2}L-L��$������ţ�ٵڶ����ɣ���
$mg+2k��\sqrt{2}L-L��cos45��=ma$
���$a=g+\frac{��2-\sqrt{2}��kL}{m}$����C��ȷ��
D��Բ����A��B���̣����ݹ��ܹ�ϵ�����ٵ���������ת��Ϊ���ܣ�$mg2L=\frac{1}{2}m{v}_{\;}^{2}$
���$v=2\sqrt{gL}$����D��ȷ��
��ѡ��CD
���� ���⿼����ţ���˶����ɣ��ؼ�����ȷ�о������������������ע�Ȿ���е��ɵĵ����DZ�������ĩλ�õ��ɵ��α�����ȣ�����������ȣ�ͬʱע��Բ����ϸ��֮����ѹ��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | �٢� | B�� | �٢� | C�� | �ڢ� | D�� | �ڢ� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
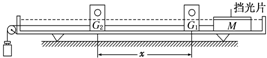
��Ŀ���������� ��Դ�� ���ͣ�ʵ����
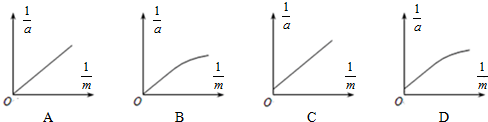
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ���ĵ���Ť��ʵ��Ӧ����Ԫ��˼�뷽�� | |
| B�� | E=$\frac{F}{q}$�����˱�ֵ����ķ��� | |
| C�� | �ٶ�v=$\frac{��x}{Vt}$������t�dz�Сʱ�ɱ�ʾtʱ�̵�˲ʱ�ٶȣ�Ӧ���˼���˼�뷽�� | |
| D�� | ��̽�����ٶȡ�������������֮���ϵ��ʵ���У�Ӧ���˿��Ʊ����� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
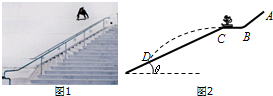
 ٤�������о����������˶�ʱ����������ʵ�飮����һ��ͭ���������С���ɺ��Բ��ƣ���б�����ɾ�ֹ��ʼ���£������ظ������ϰٴ�ʵ�飮����ij��ʵ����٤�������������ģ���б������ȡ����λ��A��B��C����ͼ��ʾ����С��ֱ���A��B��Cλ�ôӾ�ֹ���£�A��B��C��б��˵ľ���ֱ�Ϊxl��x2��x3��С����A��B��C�˶���б��˵�ʱ��ֱ�Ϊt1��t2��t3���ٶȷֱ�Ϊvl��v2��v3�������й�ϵʽ����ȷ������٤��������֤��С���ع⻬б�������˶����ȱ���ֱ���˶����ǣ�������
٤�������о����������˶�ʱ����������ʵ�飮����һ��ͭ���������С���ɺ��Բ��ƣ���б�����ɾ�ֹ��ʼ���£������ظ������ϰٴ�ʵ�飮����ij��ʵ����٤�������������ģ���б������ȡ����λ��A��B��C����ͼ��ʾ����С��ֱ���A��B��Cλ�ôӾ�ֹ���£�A��B��C��б��˵ľ���ֱ�Ϊxl��x2��x3��С����A��B��C�˶���б��˵�ʱ��ֱ�Ϊt1��t2��t3���ٶȷֱ�Ϊvl��v2��v3�������й�ϵʽ����ȷ������٤��������֤��С���ع⻬б�������˶����ȱ���ֱ���˶����ǣ�������| A�� | $\frac{{v}_{1}}{{t}_{1}}$=$\frac{{v}_{2}}{{t}_{2}}$=$\frac{{v}_{3}}{{t}_{3}}$ | B�� | $\frac{{v}_{1}}{2}$=$\frac{{v}_{2}}{2}$=$\frac{{v}_{3}}{2}$ | ||
| C�� | $\frac{{x}_{1}}{{t}_{1}^{2}}$=$\frac{{x}_{2}}{{t}_{2}^{2}}$=$\frac{{x}_{3}}{{t}_{3}^{2}}$ | D�� | x1-x2=x2-x3 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
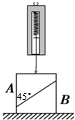 ����Ϊ4mg���ȳ���������г���ȵ�A��B�����֣����������н�Ϊ45�㣬��ͼ��ʾ���Ų�����ˮƽ�����ϣ����õ��ɳ���ֱ���������A���϶ˣ����ɳ�ʾ��Ϊmg������װ�ñ��־�ֹ��������
����Ϊ4mg���ȳ���������г���ȵ�A��B�����֣����������н�Ϊ45�㣬��ͼ��ʾ���Ų�����ˮƽ�����ϣ����õ��ɳ���ֱ���������A���϶ˣ����ɳ�ʾ��Ϊmg������װ�ñ��־�ֹ��������| A�� | ������������ܴ��ھ�Ħ���� | B�� | ���Ե����ѹ������3mg | ||
| C�� | A��B��ѹ����СΪmg | D�� | A��B֮�侲Ħ������СΪ$\frac{\sqrt{2}}{2}$mg |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��

| A�� | �����˶��Ĺ켣���� | |
| B�� | �����˶���ʱ�� | |
| C�� | ײ��˲��Ļ�е�� | |
| D�� | ײ��˲���ٶȷ�����ײ��������ƽ��ļн� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | �����˶��ٶȵĴ�С�����ܲ��� | B�� | �����ܺ������ò������������˶� | ||
| C�� | �������˶����岻һ���м��ٶ� | D�� | �����˶�һ���DZ����˶� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com