
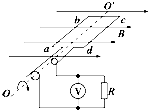
 ��ͼ��ʾΪС����ת����ʽ�����������ԭ��ͼ���������Ȧ�ڴŸ�Ӧǿ��ΪB����ǿ�ų����ƴ�ֱ�ڴų�����Ĺ̶���OO���Խ��ٶȦ�����ת������Ȧ�����ΪS������Ϊn����Ȧ�ܵ���Ϊr����Ȧ�����˾��������͵�ˢ�����R���ӣ������R�����Ľ�����ѹ��Ϊ����������t=0ʱ�̣���Ȧƽ����ų�����ƽ�У�������˵����ȷ���ǣ�������
��ͼ��ʾΪС����ת����ʽ�����������ԭ��ͼ���������Ȧ�ڴŸ�Ӧǿ��ΪB����ǿ�ų����ƴ�ֱ�ڴų�����Ĺ̶���OO���Խ��ٶȦ�����ת������Ȧ�����ΪS������Ϊn����Ȧ�ܵ���Ϊr����Ȧ�����˾��������͵�ˢ�����R���ӣ������R�����Ľ�����ѹ��Ϊ����������t=0ʱ�̣���Ȧƽ����ų�����ƽ�У�������˵����ȷ���ǣ�������| A�� | ��������������ĵ綯�Ƶ����ֵEm=nBS�� | |
| B�� | ������ѹ����ʾ��Ϊ$\frac{\sqrt{2}nRBS��}{2��R+r��}$ | |
| C�� | ��Ȧ��t=0ʱ�̿�ʼת��90��Ĺ����У�ͨ������ĵ����Ϊ$\frac{��nBS}{2\sqrt{2}��R+r��}$ | |
| D�� | ��Ȧ��t=0ʱ�̿�ʼת��90��Ĺ����У��������������Ϊ$\frac{2{n}^{2}��R{B}^{2}{S}^{2}}{�У�R+r��}$ |
���� ��������������綯�Ƶ����${E}_{m}^{\;}=nBS��$��������ѹ����ʾ����·�˵�ѹ��Чֵ��ͨ������ĵ���Ϊ$q=n\frac{����}{R+r}$���������������Ϊ$Q={I}_{\;}^{2}R��\frac{T}{4}$
��� �⣺A����������������綯�Ƶ����ֵΪ��${E}_{m}^{\;}=nBS��$����A��ȷ��
B��������ѹ���������ǵ���R���˵ĵ�ѹ���綯�Ƶ���ЧֵΪ��$E=\frac{{E}_{m}^{\;}}{\sqrt{2}}=\frac{nBS��}{\sqrt{2}}$������Ϊ��$I=\frac{E}{R+r}=\frac{nBS��}{\sqrt{2}��R+r��}$��������ѹ����ʾ��Ϊ��$U=IR=\frac{nBS��R}{\sqrt{2}��R+r��}=\frac{\sqrt{2}nRBS��}{2��R+r��}$����B��ȷ��
C����Ȧ��t=0ʱ�̿�ʼת��90��Ĺ����У���Ȧת��$\frac{T}{4}$��$\overline{E}=n\frac{����}{��t}$��ƽ������$\overline{I}=\frac{\overline{E}}{R+r}$������$q=\overline{I}•��t=n\frac{����}{R+r}$������=BS��ͨ������ĵ����Ϊ��$q=n\frac{BS}{R+r}$����C����
D�����������������$Q={I}_{\;}^{2}R\frac{T}{4}=��\frac{nBS��}{\sqrt{2}��R+r��}��_{\;}^{2}R��\frac{��}{2��}$=$\frac{��{n}_{\;}^{2}{B}_{\;}^{2}{S}_{\;}^{2}��R}{4��R+r��_{\;}^{2}}$����D����
��ѡ��AB
���� ���⿼���˽�����ķ�ֵ����Чֵ�����ں�Ƶ�ʵĹ�ϵ����ס��������õ綯�Ƶ�ƽ��ֵ������������Чֵ



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | �ʵ�͵�����ͬһ��˼�뷽�� | |
| B�� | ���ġ������������˵�Ч˼�� | |
| C�� | ٤������С����б���ϵ��˶���֤���ٶ���λ�Ƴ����� | |
| D�� | ţ�ٵ�һ������������˼ά����ʵ���з����IJ����������ʵ��ֱ��֤�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ������Ϊm�������ڴֲ�б�����Լ��ٶ�a�����»�����1���ּ�һ������F�����������ϣ���F����������ģ��ҷ�����ֱ���£���֮������ļ��ٶȽ�A��
��ͼ������Ϊm�������ڴֲ�б�����Լ��ٶ�a�����»�����1���ּ�һ������F�����������ϣ���F����������ģ��ҷ�����ֱ���£���֮������ļ��ٶȽ�A���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
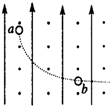
 ����ֻ�ڵ糡����������a���˶���b��Ĺ켣��ͼ��������ʾ��ͼ��һ��ƽ���Ҿ�����ȵ�ʵ�߿����ǵ糡�ߣ�Ҳ�����ǵ����棬�����ж�����ȷ���ǣ�������
����ֻ�ڵ糡����������a���˶���b��Ĺ켣��ͼ��������ʾ��ͼ��һ��ƽ���Ҿ�����ȵ�ʵ�߿����ǵ糡�ߣ�Ҳ�����ǵ����棬�����ж�����ȷ���ǣ�������| A�� | ����ͼ��ʵ���ǵ糡���ǵ����棬a��ĵ��ƶ���b��� | |
| B�� | ����ͼ��ʵ���ǵ糡���ǵ����棬a��ĵ糡ǿ�ȶ���b��С | |
| C�� | ���ͼ��ʵ���ǵ����棬������a�㶯�ܽ���b��С | |
| D�� | ���ͼ��ʵ���ǵ糡�ߣ�������a�㶯�ܽ���b��С |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 ��ͼ��ʾ���ڿռ������ˮƽ�������ǿ�ų�����ֱ�������ǿ�糡���糡ǿ��ΪE���Ÿ�Ӧǿ��ΪB����ij���ɾ�ֹ�ͷ�һ������Һ��a�����˶�����͵㴦��ǡ��һ��ԭ��������ͼʾλ�õ�Һ��b��ײ��ײ����Һ�κ�Ϊһ�壬��ԭ�ٵ�$\frac{2}{3}$��ˮƽ������ֱ���˶�����֪Һ��a������Һ��b����m��2����Һ��a�����������Һ��b���������q��4������a��b�Ĵ������ʺͳ�ʼλ��֮��ĸ߶Ȳ�hΪ����a��b֮��ľ��������Բ��ƣ��������ٶ�Ϊg����������
��ͼ��ʾ���ڿռ������ˮƽ�������ǿ�ų�����ֱ�������ǿ�糡���糡ǿ��ΪE���Ÿ�Ӧǿ��ΪB����ij���ɾ�ֹ�ͷ�һ������Һ��a�����˶�����͵㴦��ǡ��һ��ԭ��������ͼʾλ�õ�Һ��b��ײ��ײ����Һ�κ�Ϊһ�壬��ԭ�ٵ�$\frac{2}{3}$��ˮƽ������ֱ���˶�����֪Һ��a������Һ��b����m��2����Һ��a�����������Һ��b���������q��4������a��b�Ĵ������ʺͳ�ʼλ��֮��ĸ߶Ȳ�hΪ����a��b֮��ľ��������Բ��ƣ��������ٶ�Ϊg����������| A�� | a�����磬b������ | B�� | a�����磬b������ | C�� | h=$\frac{3{m}^{2}g}{2{B}^{2}{q}^{2}}$ | D�� | h=$\frac{2{m}^{2}g}{3{B}^{2}{q}^{2}}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | �����ڶ����еĽ��ٶ���� | B�� | �����ڶ����е����ٶ���� | ||
| C�� | ������ĺڶ���ת�뾶С | D�� | �����ڶ����е����ļ��ٶ���� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
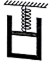 ��ͼ��ʾ��һ�ᵯ�ɵ��϶˹̶����컨���ϣ��¶˺�һ���������������һϸ�������컨��ͻ���֮�䣬���������ڷ����һ���������壬������������Ħ���ƶ�����©�������¶�ΪT1ʱ�����ɴ�����Ȼ���ȣ������ڲ�������ľ���ΪL��Ȼ�����ϸ�������������¶ȿ�ʼ����������T2����ϵͳ�ﵽ���ȶ��Ĺ���������ų�����Q����֪��������ΪM�����������ΪS������ѹǿΪp0���������ٶ�Ϊg������ʼ��û���������ף���
��ͼ��ʾ��һ�ᵯ�ɵ��϶˹̶����컨���ϣ��¶˺�һ���������������һϸ�������컨��ͻ���֮�䣬���������ڷ����һ���������壬������������Ħ���ƶ�����©�������¶�ΪT1ʱ�����ɴ�����Ȼ���ȣ������ڲ�������ľ���ΪL��Ȼ�����ϸ�������������¶ȿ�ʼ����������T2����ϵͳ�ﵽ���ȶ��Ĺ���������ų�����Q����֪��������ΪM�����������ΪS������ѹǿΪp0���������ٶ�Ϊg������ʼ��û���������ף����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
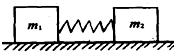 ��ͼ��ʾ����ľ��m1��m2���ڱ�ѹ�������ʵ������ˣ�����ϸ��˿�̶������û��潫��˿�ն�ʱ���ڵ�����������ľ�鱻��������֪m2=$\frac{1}{2}$m1�����ٶ���ľ��ʼ���ܵ���ȵĺ㶨�����������뵯���������ˮƽ����ֱ��˶�����s1��s2��ֹͣ��������
��ͼ��ʾ����ľ��m1��m2���ڱ�ѹ�������ʵ������ˣ�����ϸ��˿�̶������û��潫��˿�ն�ʱ���ڵ�����������ľ�鱻��������֪m2=$\frac{1}{2}$m1�����ٶ���ľ��ʼ���ܵ���ȵĺ㶨�����������뵯���������ˮƽ����ֱ��˶�����s1��s2��ֹͣ��������| A�� | s1=4s2 | B�� | s1=s2 | C�� | s1=$\frac{1}{2}$s2 | D�� | s1=2s2 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
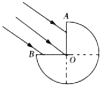 ���Ϊd���뾶ΪR����Բ�����ȥ$\frac{1}{4}$����������ͼ��ʾ��һ��ƽ�й���OA��OB��45����䵽OA��OB���ϣ��ù����պø���OA��OB�棬����Թ��������Ϊn=$\sqrt{2}$������������Ĺ����䵽Բ�������������������²����Ƿ�����ߣ���
���Ϊd���뾶ΪR����Բ�����ȥ$\frac{1}{4}$����������ͼ��ʾ��һ��ƽ�й���OA��OB��45����䵽OA��OB���ϣ��ù����պø���OA��OB�棬����Թ��������Ϊn=$\sqrt{2}$������������Ĺ����䵽Բ�������������������²����Ƿ�����ߣ����鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com