
 在做“用单摆测定重力加速度”的实验中.
在做“用单摆测定重力加速度”的实验中.| l/m | 0.4 | 0.5 | 0.8 | 0.9 | 1.0 | 1.2 |
| T/s | 1.26 | 1.42 | 1.79 | 1.90 | 2.00 | 2.20 |
| T2/s2 | 1.59 | 2.02 | 3.20 | 3.61 | 4.00 | 4.84 |
分析 (1)根据单摆的周期公式得出重力加速度的表达式,逐项分析,得出重力加速度测量值偏大的原因;
(2)根据给出的数据,在坐标系中画出相应的图线,然后从中选取合适的点,求出图线的斜率,然后结合重力加速度的表达式,求出重力加速度;
(3)结合单摆在最大摆角θ较大时周期公式推导出与T的一次函数关系式,从而分析判断.
解答  解:(1)根据$T=2π\sqrt{\frac{L}{g}}$得,g=$\frac{4{π}^{2}L}{{T}^{2}}$,
解:(1)根据$T=2π\sqrt{\frac{L}{g}}$得,g=$\frac{4{π}^{2}L}{{T}^{2}}$,
A、测摆长时,忘记了摆球的半径,则摆长的测量值偏小,则重力加速度的测量值偏小.故A错误;
B、摆线上端悬点未固定,振动中出现松动,使摆线长度增加了,则摆长的测量值偏小,重力加速度测量值偏大.故B错误;
C、开始计时时,秒表过早按下,则周期的测量值偏大,重力加速度的测量值偏小.故C错误;
D、实验中误将49次全振动次数记为50次,则周期测量值偏小,重力加速度测量值偏大.故D正确.
故选:D.
(2)以摆长L为横坐标,T2为纵坐标,作出T2-L图线如图;
根据单摆的周期公式$T=2π\sqrt{\frac{L}{g}}$得,g=$\frac{4{π}^{2}L}{{T}^{2}}$,
所以图线的斜率k=$\frac{{T}^{2}}{L}=\frac{4{π}^{2}}{g}$
由图可得:k=$\frac{4.8}{1.20}=4$
所以:g=$\frac{4{π}^{2}}{k}=9.86m/{s}^{2}$
(3)实验中得到的线性图线,根据为T=2π(1+$\frac{1}{4}$sin2$\frac{θ}{2}$)$\sqrt{\frac{l}{g}}$,得sin2$\frac{θ}{2}$=$\frac{2}{π\sqrt{\frac{l}{g}}}T-4$,所以sin2$\frac{θ}{2}$与T成一次函数关系,
所以图乙中的纵轴表示的是sin2$\frac{θ}{2}$,图线延长后与横轴交点的横坐标位$2π\sqrt{\frac{l}{g}}$
故答案为:(1)D;
(2)图象如图,9.86;
(3)sin2$\frac{θ}{2}$,$2π\sqrt{\frac{l}{g}}$.
点评 解决本题的关键掌握单摆的周期公式,会通过图象法求解重力加速度,本题第三问关键根据表达式分析出$(sin\frac{θ}{2})^{2}$与T的一次函数关系式


科目:高中物理 来源: 题型:选择题
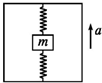 如图所示,将质量为m=0.1kg的物体用两个完全一样的竖直轻弹簧固定在升降机内,当升降机以4m/s2的加速度加速向上运动时,上面弹簧对物体的拉力为0.4N;当升降机和物体都以8m/s2的加速度向上运动时,下面弹簧对物体的支持力为( )
如图所示,将质量为m=0.1kg的物体用两个完全一样的竖直轻弹簧固定在升降机内,当升降机以4m/s2的加速度加速向上运动时,上面弹簧对物体的拉力为0.4N;当升降机和物体都以8m/s2的加速度向上运动时,下面弹簧对物体的支持力为( )| A. | 0.6 N | B. | 0.8 N | C. | 1.0 N | D. | 1.2 N |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 动能减少了Fh | B. | 重力势能减少了mgh | ||
| C. | 机械能减少了(F-mg)h | D. | 机械能减少了Fh |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 爱因斯坦通过实验发现通电导线周围存在磁场,并提出了判断磁场方向的左手定则 | |
| B. | 奥斯特通过近十年的艰苦探索终于发现了“磁生电”的规律 | |
| C. | 法拉第通过实验发现了电磁感应现象,并总结出了感应电流方向的判断方法 | |
| D. | 变化的磁场能够在周围空间产生电场,是麦克斯韦最先提出的基本假设之一 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 法拉第发现了电流的磁效应 | |
| B. | 奥斯特发现了电磁感应定律 | |
| C. | 库仑发现了点电荷间的作用规律 | |
| D. | 洛伦兹发现了磁场对电流的作用规律 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,两根足够长的光滑平行金属导轨MN、PQ间距为L=0.5m,其电阻不计,两导轨及其构成的平面与水平面成30°角.完全相同的两金属棒ab、cd分别垂直导轨放置,每棒两端都与导轨始终良好接触,已知两棒质量均为m=0.02kg,电阻均为R=0.1Ω,整个装置处在垂直于导轨平面向上的匀强磁场中,磁感应强度B=0.2T,棒ab在平行于导轨向上的力F作用下,沿导轨向上匀速运动,而棒cd恰好能够保持静止.g取10m/s2,
如图所示,两根足够长的光滑平行金属导轨MN、PQ间距为L=0.5m,其电阻不计,两导轨及其构成的平面与水平面成30°角.完全相同的两金属棒ab、cd分别垂直导轨放置,每棒两端都与导轨始终良好接触,已知两棒质量均为m=0.02kg,电阻均为R=0.1Ω,整个装置处在垂直于导轨平面向上的匀强磁场中,磁感应强度B=0.2T,棒ab在平行于导轨向上的力F作用下,沿导轨向上匀速运动,而棒cd恰好能够保持静止.g取10m/s2,查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,光滑的“Π”形金属导体框竖直放置,质量为m的金属棒MN与框架接触良好,磁感应强度分别为B1、B2的有界匀强磁场方向相反,但均垂直于框架平面,分别处在abcd和cdef区域.现从图示位置由静止释放金属棒MN,金属棒进入磁场区域abcd后恰好做匀速运动.下列说法正确的有( )
如图所示,光滑的“Π”形金属导体框竖直放置,质量为m的金属棒MN与框架接触良好,磁感应强度分别为B1、B2的有界匀强磁场方向相反,但均垂直于框架平面,分别处在abcd和cdef区域.现从图示位置由静止释放金属棒MN,金属棒进入磁场区域abcd后恰好做匀速运动.下列说法正确的有( )| A. | 若B2=B1,则金属棒进入cdef区域后将加速下滑 | |
| B. | 若B2=B1,则金属棒进入cdef区域后仍将保持匀速下滑 | |
| C. | 若B2<B1,则金属棒进入cdef区域后可能先加速后匀速下滑 | |
| D. | 若B2>B1,则金属棒进入cdef区域后可能先加速后匀速下滑 |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com