一辆汽车停在十字路口等候绿灯,当绿灯亮时汽车以2m/s2的加速度开始行驶,恰在这时一辆自行车以8m/s的速度匀速从汽车旁向同一方向驶去,从后边超过汽车.试求:
(1)汽车从路口开动后,经过多少时间追上了自行车?
(2)汽车从路口开动后,在追上自行车之前经过多长时间两车相距最远?此时距离是多少?
解:(1)设汽车从路口开动后,经过t
1时间追上自行车,此时两车的位移相等,则有:
v
自t
1=

解得:t
1=8s
(2)当汽车与自行车的速度相等时,两者相距最远,设经过的时间为t
2,此时有:
v
自=at
2
解得:

=
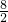
s=4s
两车相距的最大距离为:S=v
自t
2-
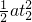
=8×4m-
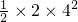
m=16m
答:(1)汽车从路口开动后,经过8s时间追上了自行车;
(2)汽车从路口开动后,在追上自行车之前经过4s时间两车相距最远,此时距离是16m.
分析:(1)由题,自行车以8m/s的速度做匀速运动,汽车以2m/s
2的加速度做匀加速运动,两车从同一位置经过,当位移相等时,汽车追上自行车,根据位移公式求解时间;
(2)汽车从路口开动后,速度先小于自行车的速度,后大于自行车的速度,两车的距离先增大后减小,当两车的速度相等时,相距最远,根据速度相等,由速度公式求出时间,由位移公式求出两车间的距离.
点评:本题是匀加速运动追及匀速运动的问题,在分别研究两车运动情况的基础上,关键要抓住两车之间的关系,比如速度关系、位移关系.


 =
=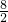 s=4s
s=4s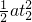 =8×4m-
=8×4m-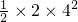 m=16m
m=16m
