
 如图所示,将质量均为m、厚度不计的两物块A、B用轻质弹簧相连接.第一次只用手托着B物块于H高度,A在弹簧的作用下处于静止,将该状态下的弹簧锁定,此时弹簧的弹性势能为Ep.现由静止开始释放A、B,B物块刚要着地前瞬间,将弹簧瞬间解除锁定(解除锁定无机械能损失),B物块着地后速度立即变为0,在随后的过程中B物块恰能离开地面但不继续上升.第二次用手拿着A、B两物块,使得弹簧竖直并处于原长状态,此时物块B离地面的距离也为H,然后由静止同时释放A、B,B物块着地后速度同样立即变为0.求第二次释放A、B后,B刚要离地时A的速度大小.
如图所示,将质量均为m、厚度不计的两物块A、B用轻质弹簧相连接.第一次只用手托着B物块于H高度,A在弹簧的作用下处于静止,将该状态下的弹簧锁定,此时弹簧的弹性势能为Ep.现由静止开始释放A、B,B物块刚要着地前瞬间,将弹簧瞬间解除锁定(解除锁定无机械能损失),B物块着地后速度立即变为0,在随后的过程中B物块恰能离开地面但不继续上升.第二次用手拿着A、B两物块,使得弹簧竖直并处于原长状态,此时物块B离地面的距离也为H,然后由静止同时释放A、B,B物块着地后速度同样立即变为0.求第二次释放A、B后,B刚要离地时A的速度大小. 分析 设弹簧的劲度系数为k,第一次释放AB前,弹簧向上产生的弹力与A的重力平衡,求出弹簧压缩量,第一次释放AB后,B刚要离地时弹簧产生向上的弹力与B的重力平衡,求出伸长量,第二次释放AB后,在B刚要离地时弹簧产生向上的弹力与B的重力平衡,求出伸长量,对A、B和弹簧组成的系统由机械能守恒即可解题.
解答 解:二次释放A、B后,A、B均先做自由落体运动.设B着地前瞬间的速度为v1,由$2gH=v_1^2$,得:
${v_1}=\sqrt{2gH}$ ①
设弹簧的劲度系数为k,第一次释放A、B前,弹簧弹力与A的重力平衡,设弹簧的形变量(压缩)为△x1,有:
$△{x}_{1}=\frac{mg}{k}$
二次释放A、B后,在B刚要离地时,弹簧弹力与B的重力平衡,设弹簧的形变量(伸长)为△x2,有:
$△{x}_{2}=\frac{mg}{k}$
因△x1=△x2,故弹簧在这两个状态下的弹性势能相等,都为Ep.
二次释放,从B着地后到B刚要离地的过程,A与弹簧组成的系统机械能均守恒,对应第二次,有$\frac{1}{2}mv_1^2=mg△{x_2}+{E_P}+\frac{1}{2}m{v^2}$ ②
对应第一次,有:
$\frac{1}{2}mv_1^2+{E_P}=mg({△{x_1}+△{x_2}})+{E_P}$③
由①②③解得:
$v=\sqrt{gH-\frac{{2{E_P}}}{m}}$
答:第二次释放A、B后,B刚要离地时A的速度大小为$\sqrt{gH-\frac{2{E}_{P}}{m}}$.
点评 本题主要考查了动能定理及机械能守恒定律的应用,要求同学们能正确分析物体的运动情况,选择正确的过程及研究对象,不难.


科目:高中物理 来源: 题型:解答题
 如图所示,半径为r的光滑圆管形轨道AB部分平直,BC部分是处于竖直平面内半径为R的半圆,r远小于R.有一质量m,半径比r略小的光滑小球以水平初速度v0射入圆管中:
如图所示,半径为r的光滑圆管形轨道AB部分平直,BC部分是处于竖直平面内半径为R的半圆,r远小于R.有一质量m,半径比r略小的光滑小球以水平初速度v0射入圆管中:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 农民在精选谷种时,常用一种叫“风车”的农具进行分选.在同一风力作用下,谷种和瘪谷(空壳)都从洞口水平飞出,结果谷种和瘪谷落地点不同,自然分开,M处是瘪谷,N处是谷种,如图所示.若不计空气阻力,对这一现象,下列分析正确的是( )
农民在精选谷种时,常用一种叫“风车”的农具进行分选.在同一风力作用下,谷种和瘪谷(空壳)都从洞口水平飞出,结果谷种和瘪谷落地点不同,自然分开,M处是瘪谷,N处是谷种,如图所示.若不计空气阻力,对这一现象,下列分析正确的是( )| A. | 谷种飞出洞口时的速度比瘪谷飞出洞口时的速度小些 | |
| B. | 谷种和瘪谷飞出洞口后水平方向都做匀速直线运动 | |
| C. | 瘪谷运动过程中加速度较小 | |
| D. | 瘪谷从飞出洞口到落地所用的时间较长 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
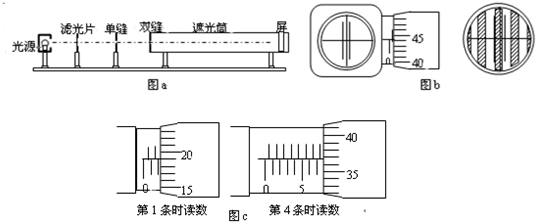
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 卫星的轨道半径为$\root{3}{{\frac{{GM{T^2}}}{{4{π^2}}}}}$ | |
| B. | 卫星的运行速度小于第一宇宙速度 | |
| C. | 卫星运行时受到的向心力大小为G$\frac{Mm}{R^2}$ | |
| D. | 卫星运行的向心加速度小于地球表面的重力加速度 |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 汽车的加速性能是汽车技术性能指标上的一个参考值,用如图所示的装置可以测量汽车在水平路面上作匀加速直线运动的加速度.该装置是在矩形车厢前、后壁上各安装一个压力传感器.用两根完全一样的轻质弹簧夹着一个质量为2.0kg的滑块,两轻质弹簧的另一端分别压在传感器a、b上,其压力大小可直接从传感器的显示屏上读出.现将装置沿运动方向固定在汽车上(弹簧与滑块均在水平方向,且滑块与水平面无摩擦),b在前,a在后,当汽车静止时,传感器a、b的示数均为10N.(g=10m/s2)
汽车的加速性能是汽车技术性能指标上的一个参考值,用如图所示的装置可以测量汽车在水平路面上作匀加速直线运动的加速度.该装置是在矩形车厢前、后壁上各安装一个压力传感器.用两根完全一样的轻质弹簧夹着一个质量为2.0kg的滑块,两轻质弹簧的另一端分别压在传感器a、b上,其压力大小可直接从传感器的显示屏上读出.现将装置沿运动方向固定在汽车上(弹簧与滑块均在水平方向,且滑块与水平面无摩擦),b在前,a在后,当汽车静止时,传感器a、b的示数均为10N.(g=10m/s2)查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
 在“探究弹力和弹簧伸长量的关系”实验中.
在“探究弹力和弹簧伸长量的关系”实验中.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com