
 ��ͼ��ʾ��������ͬ��ƽ�н���ֱ�����ֱ���ã��϶��õ��߽�һ��ֵ���裬�¶˹̶���ˮƽ��Ե�����ϣ���������̶�һ�����ɣ�����ֱ��abͨ�������������ڹ���ϣ���MNPQ֮��ֲ��Ŵ�ֱ������������ǿ�ų���������ѹ��ʹ���ɴ���ѹ��״̬��������˱��������뵯�ɺ����ų�������PQ�����������Ȼ���ٷ��شų������ܴӱ߽�MN�������˺��ٽ���ų�����ab������Ħ������С����ڸ�������$\frac{5}{13}$������֪�������˶�ʱ���մ���PQʱ���ٶ��Ǹմ���MNʱ�ٶȵ�һ�룬�˴�PQ���������߶ȣ�δ��������϶ˣ��Ǵų��߶ȵ�n�����������˶�ʱ��һ����ų�����������ֱ���˶�������ֵ�����ⲻ������һ�е��裬��֪�������ٶ�Ϊg����
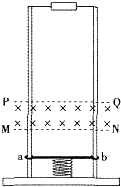
��ͼ��ʾ��������ͬ��ƽ�н���ֱ�����ֱ���ã��϶��õ��߽�һ��ֵ���裬�¶˹̶���ˮƽ��Ե�����ϣ���������̶�һ�����ɣ�����ֱ��abͨ�������������ڹ���ϣ���MNPQ֮��ֲ��Ŵ�ֱ������������ǿ�ų���������ѹ��ʹ���ɴ���ѹ��״̬��������˱��������뵯�ɺ����ų�������PQ�����������Ȼ���ٷ��شų������ܴӱ߽�MN�������˺��ٽ���ų�����ab������Ħ������С����ڸ�������$\frac{5}{13}$������֪�������˶�ʱ���մ���PQʱ���ٶ��Ǹմ���MNʱ�ٶȵ�һ�룬�˴�PQ���������߶ȣ�δ��������϶ˣ��Ǵų��߶ȵ�n�����������˶�ʱ��һ����ų�����������ֱ���˶�������ֵ�����ⲻ������һ�е��裬��֪�������ٶ�Ϊg�������� ��1���Ը�ab����PQ���������½����̣��ֱ����ö��ܶ�����ʽ�������v1��v2֮�ȣ�
��2������ab����������Ĺ��̣��ֱ����ö��ܶ�����ʽ������ÿ˷�����������֮�ȣ����ɵõ������ĵ���֮��Q1��Q2
��� �⣺��1�����ab��������ߵ��PQ�ľ���Ϊh���ɶ��ܶ����У�
������-��mg+Ff��h=0-$\frac{1}{2}$mv12����
�½��Σ�mgh-Ffh=$\frac{1}{2}$mv22-0����
Ff=$\frac{5}{13}mg$
��ã�v1��v2=3��2��
��2������ab��������ߵ��PQ�ľ���Ϊh����ų��߶�Ϊ$\frac{h}{n}$���ɶ��ܶ����ã�
-��mg+Ff����h+$\frac{h}{n}$��-W1=0-$\frac{1}{2}$mv02
ͬ�����ڷ��ؽΣ���mg-Ff����h+$\frac{h}{n}$��-W2=mv22-0
������ʽ��ã�$\frac{{Q}_{1}}{{Q}_{2}}$=$\frac{{W}_{1}}{{W}_{2}}$=$\frac{9��3n-1��}{4}$��
�𣺣�1�������ϴ���PQʱ���ٶ��뷵��PQʱ���ٶȴ�С֮��v1��v2=3��2��
��2�������ϡ��������δ�Խ�ų��Ĺ����в����ĵ���֮��Q1��Q2=9��3n-1����4
���� ����Ĺ��̱Ƚϸ��ӣ�����ѧ���Ÿ�Ӧ���ۺϣ����ö��ܶ���ʱ��Ҫע����ȷ���о����������̣�Ӧ��ţ�ٵڶ������밲������ʽ������ȷ����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
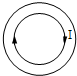
| A�� | ����ʱ�뷽��ĸ�Ӧ������Բ��B���������ŵ����� | |
| B�� | ��˳ʱ�뷽��ĸ�Ӧ������Բ��B���������ŵ����� | |
| C�� | ����ʱ�뷽��ĸ�Ӧ������Բ��B���������ŵ����� | |
| D�� | ��˳ʱ�뷽��ĸ�Ӧ������Բ��B���������ŵ����� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
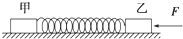 ��ͼ��ʾ���ڴֲ�ˮƽ�����мס�����ľ�飬��ˮƽ���Ķ�Ħ��������Ϊ�̣������ֱ�Ϊm1��m2���м���һԭ��ΪL������ϵ��Ϊk�����ʵ���������������ʼʱ��ľ�����ֹ�ҵ������α䣮����һˮƽ����F��F���̣�m1+m2��g��������ľ���ң�ֱ����ľ���һ�δﵽ���ٶ���ͬʱ������˵����ȷ���ǣ�������
��ͼ��ʾ���ڴֲ�ˮƽ�����мס�����ľ�飬��ˮƽ���Ķ�Ħ��������Ϊ�̣������ֱ�Ϊm1��m2���м���һԭ��ΪL������ϵ��Ϊk�����ʵ���������������ʼʱ��ľ�����ֹ�ҵ������α䣮����һˮƽ����F��F���̣�m1+m2��g��������ľ���ң�ֱ����ľ���һ�δﵽ���ٶ���ͬʱ������˵����ȷ���ǣ�������| A�� | ��ʱ���ٶȿ��ܵ����ҵ��ٶ� | |
| B�� | ��ʱ��ľ��֮��ľ���ΪL-$\frac{F{m}_{1}}{��{m}_{1}+{m}_{2}��k}$ | |
| C�� | �˽�ˮƽ��F���Ĺ����ڼ�������鶯���������뵯���������������ܺ� | |
| D�� | �˽μ���������������Ħ�����ij�����С��� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{h}{s}$ | B�� | $\frac{2h}{s}$ | C�� | $\sqrt{\frac{h}{s}}$ | D�� | $\sqrt{\frac{2h}{s}}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ������ϸ�߹�ϵ��O�㣬����OA��ֱ��OBˮƽ���������������һ�����OC��C��̶��ڵ����ϣ�����װ�ô��ھ�ֹ״̬����ʹC������ˮƽ���ƣ�ͬʱ����O��B��λ�ò��䣬װ����Ȼ���־�ֹ״̬����ϸ��OA������T1��OC������T2��ԭ������ǣ�������
��ͼ��ʾ������ϸ�߹�ϵ��O�㣬����OA��ֱ��OBˮƽ���������������һ�����OC��C��̶��ڵ����ϣ�����װ�ô��ھ�ֹ״̬����ʹC������ˮƽ���ƣ�ͬʱ����O��B��λ�ò��䣬װ����Ȼ���־�ֹ״̬����ϸ��OA������T1��OC������T2��ԭ������ǣ�������| A�� | T1��T2����С | B�� | T1��T2������ | C�� | T1����T2��С | D�� | T1��С��T2���� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | �����̫����ľ�ǵ��������� | B�� | �����̫�����ܶ� | ||
| C�� | �����ľ�DZ�����������ٶ� | D�� | $\frac{{r}_{1}^{3}}{{T}_{1}^{2}}$=$\frac{{r}_{2}^{3}}{{T}_{2}^{2}}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ��ʾ���ᵯ����˹̶�����ֱǽ�ϣ��Ҷ˽�������Ϊm1=1kg��С��飮����Ϊm2=1kg��С��������Ϊ��=37���б���ϸ�h=0.6m����ֹ��ʼ���£���б�����������ʧ�ؽ���⻬ˮƽ�棬����m1��ײ��ճ����һ�������˶�����֪С������б��Ķ�Ħ������Ϊ��=0.5��g=10m/s2��sin37��=0.6��cos37��=0.8����
��ͼ��ʾ���ᵯ����˹̶�����ֱǽ�ϣ��Ҷ˽�������Ϊm1=1kg��С��飮����Ϊm2=1kg��С��������Ϊ��=37���б���ϸ�h=0.6m����ֹ��ʼ���£���б�����������ʧ�ؽ���⻬ˮƽ�棬����m1��ײ��ճ����һ�������˶�����֪С������б��Ķ�Ħ������Ϊ��=0.5��g=10m/s2��sin37��=0.6��cos37��=0.8�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ��ʾ��M=2kg��С����ֹ�ڹ⻬��ˮƽ���ϣ�������AB���dz�L=lm�Ĵֲ�ƽ�棬BC�����ǰ뾶R=0.4m�Ĺ⻬$\frac{1}{4}$Բ�����������һ����m=lkg�Ľ����龲ֹ�ڳ����A�ˣ���������AB��Ķ�Ħ��������=0.3������Aʩ��һˮƽ���ҡ���СΪI=5N•s��˲���������С���ܻ�õ�����ٶȣ���gȡ10m/s2��
��ͼ��ʾ��M=2kg��С����ֹ�ڹ⻬��ˮƽ���ϣ�������AB���dz�L=lm�Ĵֲ�ƽ�棬BC�����ǰ뾶R=0.4m�Ĺ⻬$\frac{1}{4}$Բ�����������һ����m=lkg�Ľ����龲ֹ�ڳ����A�ˣ���������AB��Ķ�Ħ��������=0.3������Aʩ��һˮƽ���ҡ���СΪI=5N•s��˲���������С���ܻ�õ�����ٶȣ���gȡ10m/s2���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com