
分析 (1)单摆的摆长等于摆线的长度加上小球的半径.而T=$\frac{t}{n}$ 求出周期,再根据单摆周期公式T=2$π\sqrt{\frac{L}{g}}$,即可求解.
(2)根据重力加速度的表达式分析g值偏小可能的原因.
(3)根据重力加速度的表达式和数学知识,分析T2-l图线斜率k的意义,得到g的表达式.
解答 解:(1)摆线的长度为l=L+$\frac{D}{2}$.
而周期为T=$\frac{t}{n}$,
再根据单摆周期公式T=2$π\sqrt{\frac{L}{g}}$,则有:g=$\frac{4{π}^{2}(L+\frac{D}{2})}{(\frac{t}{n})^{2}}$.
(2)A、将摆线拉得过紧,摆长偏大,则根据重力加速度的表达式g=$\frac{4{π}^{2}L}{{T}^{2}}$ 可知,测得的g值偏大.故A错误.
B、摆线上端未牢固地系于悬点,振动中出现松动,使摆线长度增加了,使周期变大了,由g=$\frac{4{π}^{2}L}{{T}^{2}}$ 可知,因不知道摆长变化,因此测得的g值偏小.故B正确.
C、开始计时时,秒表过迟按下,测得的时间偏小,周期偏小,则测得的g值偏大.故C错误.
D、实验中误将49次全振动数次数记为50次,由T=$\frac{t}{n}$求出的周期偏小,测得的g值偏大.故D错误.
故选:B.
(3)根据重力加速度的表达式g=$\frac{4{π}^{2}L}{{T}^{2}}$ 可知,
T2-l图线斜率k=$\frac{4{π}^{2}}{g}$,
则g=$\frac{4{π}^{2}}{k}$.
故答案为:(1)$\frac{4{π}^{2}(L+\frac{D}{2})}{(\frac{t}{n})^{2}}$.(2)B;(3)$\frac{4{π}^{2}}{k}$.
点评 单摆的摆长不是摆线的长度,还要加上摆球的半径.对于实验误差,要从实验原理公式进行分析,同时掌握单摆周期公式的应用,注意重力加速度的误差分析.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中物理 来源: 题型:多选题
| A. | 法拉第首先引入了场的概念 | |
| B. | 伽利略把日常生活中见到的较重的物体下落得比较快的原因归之于空气阻力对不同物体的影响不同 | |
| C. | 牛顿首先建立起来平均速度、瞬时速度以及加速度等概念 | |
| D. | 如果电场线与等势面不垂直,那么电场强度就有一个沿着等势面的分量,在等势面上移动电荷静电力就要做功,而在同一等势面上移动电荷静电力是不做功的,所以电场线与等势面垂直.这里用的逻辑方法是归纳法 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
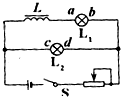
| A. | 闭合S时,L2先亮,L1后亮,最后一样亮 | |
| B. | 断开S时,L2和 L1都慢慢熄灭 | |
| C. | L1中的电流始终从a到b | |
| D. | L2中的电流始终从c到d |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题

| A. | 根据v=$\sqrt{gr}$,可知vA<vB<vC | B. | 根据万有引力定律,可知FA>FB>FC | ||
| C. | 角速度ωA>ωB>ωC | D. | 向心加速度aA>aB>aC |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 被悬挂的球B刚好与光滑水平面接触,球A以3m/s的速度向右运动,与B球相撞,碰撞后,B球向右摆动,到最高点时悬绳与竖直方向的夹角为53°,已知A球的质量是B球的2倍,悬长0.5m,则碰撞后A球的速度是多少?
被悬挂的球B刚好与光滑水平面接触,球A以3m/s的速度向右运动,与B球相撞,碰撞后,B球向右摆动,到最高点时悬绳与竖直方向的夹角为53°,已知A球的质量是B球的2倍,悬长0.5m,则碰撞后A球的速度是多少?查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,小明玩蹦蹦杆,在小明将蹦蹦杆中的弹簧向下压缩的过程中,小明的重力势能、弹簧的弹性势能的变化是( )
如图所示,小明玩蹦蹦杆,在小明将蹦蹦杆中的弹簧向下压缩的过程中,小明的重力势能、弹簧的弹性势能的变化是( )| A. | 重力势能不变 | B. | 重力势能增大 | C. | 弹性势能减少 | D. | 弹性势能增大 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
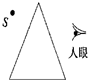 如图所示,一个小的光源S发出白光,经三棱镜分光.若人沿着折射光线的反方向观察,通过棱镜可以看到( )
如图所示,一个小的光源S发出白光,经三棱镜分光.若人沿着折射光线的反方向观察,通过棱镜可以看到( )| A. | 白光点 | B. | 光点上部红色,下部紫色 | ||
| C. | 光点上部紫色,下部红色 | D. | 看不到光源的像 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com