
 如图所示,在光滑的水平面上固定有左、右两竖直挡板,挡板间距离足够长,有一质量为M,长为L的长木板靠在左侧挡板处,另有一质量为m的小物块(可视为质点),放置在长木板的左端,已知小物块与长木板间的动摩擦因数为μ,且M>m.现使小物块和长木板以共同速度v0向右运动,设长木板与左、右挡板的碰撞中无机械能损失.试求:
如图所示,在光滑的水平面上固定有左、右两竖直挡板,挡板间距离足够长,有一质量为M,长为L的长木板靠在左侧挡板处,另有一质量为m的小物块(可视为质点),放置在长木板的左端,已知小物块与长木板间的动摩擦因数为μ,且M>m.现使小物块和长木板以共同速度v0向右运动,设长木板与左、右挡板的碰撞中无机械能损失.试求:分析 (1)选取正方向,运用动量守恒来确定共同运动的速度,根据能量守恒定律列出等式求解;
(2)m相对M向右滑动,以后M与左挡板碰撞,碰后m相对于M向左滑动,直到达到共同速度,根据动量守恒定律和能量守恒定律列出等式求解;
(3)根据能量守恒定律得求出第四次碰撞前损失的机械能.
解答 解:(1)对m,M组成的系统,选定水平向左为正方向
根据动量守恒得
Mv0-mv0=(M+m)v1
根据能量守恒定律得
μmgL1=$\frac{1}{2}$(M+m)${v}_{0}^{2}$-$\frac{1}{2}$(M+m)${v}_{1}^{2}$
解得 L1=$\frac{2{Mv}_{0}^{2}}{(M+m)μg}$
(2)上述过程中,m相对M向右滑动,以后M与左挡板碰撞,碰后m相对于M向左滑动,直到达到共同速度v2
规定向左为正方向,根据动量守恒得
(M-m)v1=(M+m)v2,
根据能量守恒定律得
μmgL2=$\frac{1}{2}$(M+m)${v}_{1}^{2}$-$\frac{1}{2}$(M+m)${v}_{2}^{2}$
解得 L2=$\frac{2{Mv}_{1}^{2}}{(M+m)μg}$
L2<L1,同理L3<L2
只要第一次碰撞后m未从M上掉下,以后就不可能掉下,
所以板长L应满足L≥$\frac{2{Mv}_{0}^{2}}{(M+m)μg}$
(3)根据能量守恒定律得
到发生第四次碰撞前,系统损失的机械能
△E=μmg(L1+L2+L3)=μmg×$\frac{2M}{(M+m)μg}$(${v}_{0}^{2}$+${v}_{1}^{2}$+${v}_{2}^{2}$)
解得:△E=149.79J
答:(1)将要发生第二次碰撞时,若小物块仍未从长木板上落下,则它应距长木板左端距离是$\frac{2{Mv}_{0}^{2}}{(M+m)μg}$;
(2)为使小物块不从长木板上落下,板长L应满足L≥$\frac{2{Mv}_{0}^{2}}{(M+m)μg}$;
(3)整个系统从开始到刚要发生第四次碰撞前损失的机械能是149.79J.
点评 本题考查动量守恒定律和能量守恒定律的应用,并多次在不同过程中使用,让同学们更能熟练的掌握规律.综合性较强,对学生的能力要求较高,要加强这方面的训练.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中物理 来源: 题型:选择题
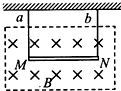 如图所示,金属棒MN两端用等长的细软导线连接后水平地悬挂.MN处在向里的水平匀强磁场中,棒中通有由M流向N的电流,此时悬线受金属棒的拉力作用.为了使悬线中的拉力减小,可采取的措施有( )
如图所示,金属棒MN两端用等长的细软导线连接后水平地悬挂.MN处在向里的水平匀强磁场中,棒中通有由M流向N的电流,此时悬线受金属棒的拉力作用.为了使悬线中的拉力减小,可采取的措施有( )| A. | 使磁场反向 | B. | 使电流反向 | C. | 增大电流强度 | D. | 减小磁感应强度 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 某实验小组利用拉力传感器、光电门等器材探究滑块“动能定理”的实验.实验装置如图所示,在滑块上安装一遮光条与拉力传感器,把滑块放在水平气垫导轨上并静止在A处,并通过定滑轮的细绳与钩码相连,光电门安装在B处.测得滑块(含遮光板和拉力传感器)质量为M、钩码总质量为m、AB之间的距离为L,当地的重力加速度为g.将滑块在图示A位置由静止释放后,拉力传感器记录下滑块在运动过程的拉力为F,光电计时器记录下遮光条通过光电门的时间分别为△t.
某实验小组利用拉力传感器、光电门等器材探究滑块“动能定理”的实验.实验装置如图所示,在滑块上安装一遮光条与拉力传感器,把滑块放在水平气垫导轨上并静止在A处,并通过定滑轮的细绳与钩码相连,光电门安装在B处.测得滑块(含遮光板和拉力传感器)质量为M、钩码总质量为m、AB之间的距离为L,当地的重力加速度为g.将滑块在图示A位置由静止释放后,拉力传感器记录下滑块在运动过程的拉力为F,光电计时器记录下遮光条通过光电门的时间分别为△t.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,水平桌面上放着一对平行金属导轨,左端与一电源相连,中间还串有一开关K.导轨上放着一根金属棒ab,空间存在着垂直导轨平面向下的匀强磁场.已知两导轨间距为d,电源电动势为E,导轨电阻及电源内阻均不计,ab棒的电阻为R,质量为m,棒与导轨间摩擦不计.闭合开关K,ab棒向右运动并从桌边水平飞出,已知桌面离地高度为h,金属棒落地点的水平位移为s.下面的结论中正确( )
如图所示,水平桌面上放着一对平行金属导轨,左端与一电源相连,中间还串有一开关K.导轨上放着一根金属棒ab,空间存在着垂直导轨平面向下的匀强磁场.已知两导轨间距为d,电源电动势为E,导轨电阻及电源内阻均不计,ab棒的电阻为R,质量为m,棒与导轨间摩擦不计.闭合开关K,ab棒向右运动并从桌边水平飞出,已知桌面离地高度为h,金属棒落地点的水平位移为s.下面的结论中正确( )| A. | 开始时ab棒离导轨右端的距离L=$\frac{m{s}^{2}gR}{4h{B}^{2}{d}^{2}E}$ | |
| B. | 磁场力对ab棒所做的功w=$\frac{m{s}^{2}g}{8h}$ | |
| C. | 磁场力对ab棒的冲量大小I=ms$\sqrt{\frac{g}{2h}}$ | |
| D. | ab棒在导轨上运动时间t=$\frac{msR}{{B}^{2}{d}^{2}e}$$\sqrt{\frac{g}{2h}}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
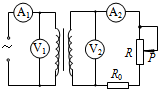 如图所示为模拟街头变压器通过降压给用户供电的示意图,变压器输入的交流电压可视为不变.变压器输出的低压交流电通过输电线输送给用户.定值电阻R0表示输电线的电阻,变阻器R表示用户用电器的总电阻.若变压器为理想变压器,电表为理想电表,则在变阻器的滑片P向上移动的过程中( )
如图所示为模拟街头变压器通过降压给用户供电的示意图,变压器输入的交流电压可视为不变.变压器输出的低压交流电通过输电线输送给用户.定值电阻R0表示输电线的电阻,变阻器R表示用户用电器的总电阻.若变压器为理想变压器,电表为理想电表,则在变阻器的滑片P向上移动的过程中( )| A. | V2示数变小 | B. | V1示数变大 | C. | A2示数变大 | D. | A1示数变小 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题

| A. | 各质点振动的周期为4s | B. | 该简谐横波的波长为4m | ||
| C. | 此时刻质点A的速度为0 | D. | 此时刻质点B的加速度为0 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图,三棱镜ABC中.∠A=90°,∠B=60°.AB的边长为.让光线从AB边的中点D以某一角度射入三棱镜,到达AC边时恰好发生全反射.已知棱镜的折射率n=$\frac{2\sqrt{3}}{3}$,不考虑光在BC边的反射,求:(真空中的光速为c)
如图,三棱镜ABC中.∠A=90°,∠B=60°.AB的边长为.让光线从AB边的中点D以某一角度射入三棱镜,到达AC边时恰好发生全反射.已知棱镜的折射率n=$\frac{2\sqrt{3}}{3}$,不考虑光在BC边的反射,求:(真空中的光速为c)查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 能量增大,数量增多 | B. | 能量减小,数量减少 | ||
| C. | 能量增大,数量减小 | D. | 能量减小,数量增多 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com