
| A. | $\frac{v_0^2}{4g}$ | B. | $\frac{3v_0^2}{4g}$ | C. | $\frac{3v_0^2}{8g}$ | D. | $\frac{v_0^2}{8g}$ |
科目:高中物理 来源: 题型:选择题
| A. | △p越大,则末动量越大 | B. | △p>0,说明动量增加 | ||
| C. | △p=0,则物体的动量不变 | D. | △p≠0,则物体的动量大小发生变化 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 某一物体的动量改变,一定是速度大小改变 | |
| B. | 某一物体的动量改变,一定是速度方向改变 | |
| C. | 某一物体的运动速度改变,其动量可能不变 | |
| D. | 物体的运动状态改变,其动量一定改变 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图,一端接有定值电阻R的足够长的平行金属导轨,放在绝缘斜面上(斜面未画出),匀强磁场垂直于导轨平面向上,导体棒ab垂直于导轨放置.现给导体棒沿斜面向上的初速度v,经过一段时间导体棒又回到原位置.在运动过程中导体棒ab始终垂直于导轨,导轨和导体棒的电阻可忽略不计.则( )
如图,一端接有定值电阻R的足够长的平行金属导轨,放在绝缘斜面上(斜面未画出),匀强磁场垂直于导轨平面向上,导体棒ab垂直于导轨放置.现给导体棒沿斜面向上的初速度v,经过一段时间导体棒又回到原位置.在运动过程中导体棒ab始终垂直于导轨,导轨和导体棒的电阻可忽略不计.则( )| A. | 在上滑过程导体棒中的电流方向由a到b | |
| B. | 回到原位置时导体棒的速度大小仍为v | |
| C. | 开始上滑和回到原位置时导体棒的加速度大小相等 | |
| D. | 上滑过程与下滑到初始位置的过程通过导体棒截面的电荷量相等 |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
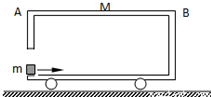 如图所示,质量为M,长为L的车厢静止在光滑水平面上,此时质量为m的木块正以水平速度v从左边进入车厢板向右运动,车厢底板粗糙,m与右壁B发生无能量损失的碰撞后又被弹回,最后又恰好停在车厢左端点A,则以下叙述中正确的是( )
如图所示,质量为M,长为L的车厢静止在光滑水平面上,此时质量为m的木块正以水平速度v从左边进入车厢板向右运动,车厢底板粗糙,m与右壁B发生无能量损失的碰撞后又被弹回,最后又恰好停在车厢左端点A,则以下叙述中正确的是( )| A. | 该过程中产生的内能为$\frac{1}{2}$mv2 | |
| B. | 车厢底板的动摩擦因数为$\frac{{M{v^2}}}{4(m+M)gL}$ | |
| C. | M的最终速度为$\frac{mv}{m+M}$ | |
| D. | m、M最终速度为零 |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
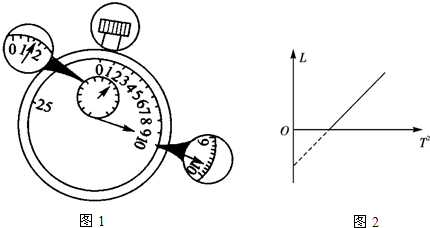
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
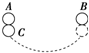 如图所示,半径相同的两个金属小球A、B带有电荷量大小相等的电荷(可视为点电荷),相隔一定的距离,两球之间的相互吸引力大小为F,今用第三个半径相同的不带电的金属小球C先后与A、B两个球接触后移开,这时,A、B两个球之间的相互作用力大小是( )
如图所示,半径相同的两个金属小球A、B带有电荷量大小相等的电荷(可视为点电荷),相隔一定的距离,两球之间的相互吸引力大小为F,今用第三个半径相同的不带电的金属小球C先后与A、B两个球接触后移开,这时,A、B两个球之间的相互作用力大小是( )| A. | $\frac{F}{8}$ | B. | $\frac{F}{4}$ | C. | $\frac{3F}{8}$ | D. | $\frac{3F}{4}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
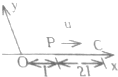
| A. | O点的振动方程为y=Acosω(t-$\frac{1}{u}$) | B. | 波的表达式为y=Acosω[t-($\frac{1}{u}$)-($\frac{x}{u}$)] | ||
| C. | 波的表达式为y=Acosω[t+($\frac{1}{u}$)-($\frac{x}{u}$)] | D. | C点的振动方程为y=Acosω(t-$\frac{3l}{u}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com