
分析 根据${C}_{n}^{2}$计算跃迁可能的种类;根据数学的组合关系计算光子的总数.
解答 解:一群氢原子均处于第5能级,在向低能级跃迁时,一共能辐射${C}_{5}^{2}=10$种不同频率的光子;
2g氢气为1mol,氢原子的个数为2mol;
由于某能级H原子向不同低能级跃迁时,所占此能级上H原子总数的比例相同,可知,处于n=5能量的氢原子向低能级跃迁的过程中,n=5→n=4、n=5→n=3、n=5→n=2、n=5→n=1共四种情况,各占$\frac{1}{4}$,所以每一种都是$\frac{1}{2}$NA个;
n=4、n=3、n=2能级的氢原子仍然向低能级跃迁,处于n=4能量的氢原子向低能级跃迁的过程中,n=4→n=3、n=4→n=2、n=4→n=1共三种情况,各占$\frac{1}{3}$,所以每一种都是$\frac{1}{2}$×$\frac{1}{3}$NA=$\frac{1}{6}$NA个;
处于n=3能量的氢原子向低能级跃迁的过程中,n=3→n=2、n=3→n=1共两种情况,各占$\frac{1}{2}$,所以每一种都是$\frac{1}{2}$×$(\frac{1}{2}+\frac{1}{6})$NA=$\frac{1}{3}$NA个;
处于n=2能量的氢原子向低能级跃迁的过程中辐射的光子的种类:$(\frac{1}{2}+\frac{1}{6}+\frac{1}{3}){N}_{A}={N}_{A}$个
所以当所有氢原子跃迁到基态时,辐射的光子总数为:N=($4×\frac{1}{2}+3×\frac{1}{6}+2×\frac{1}{3}+1$)NA=$\frac{25}{6}$NA
故答案为:10,$\frac{25}{6}$NA
点评 解决本题的关键知道光子能量与能级差的关系,即Em-En=hv,以及知道跃迁种类的判定.


科目:高中物理 来源: 题型:填空题
 质量一定的理想气体完成如图所示的循环,其中A→B过程是绝热过程,B→C过程是等温过程,则A→B过程气体内能减小(选填“增加”、“减小”或“不变”),从状态A经B、C再回到状态A的过程中,气体吸收的热量大于放出的热量(选填“大于”、“小于”或“等于”)
质量一定的理想气体完成如图所示的循环,其中A→B过程是绝热过程,B→C过程是等温过程,则A→B过程气体内能减小(选填“增加”、“减小”或“不变”),从状态A经B、C再回到状态A的过程中,气体吸收的热量大于放出的热量(选填“大于”、“小于”或“等于”)查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 该行星的公转周期为2πr$\sqrt{\frac{r}{Gm}}$ | |
| B. | 该行星表面的重力加速度为$\frac{Gm}{{R}^{2}}$ | |
| C. | 该行星的第一宇宙速度为$\sqrt{\frac{Gm}{R}}$ | |
| D. | 该行星绕恒星做匀速圆周运动的线速度大小为 $\sqrt{\frac{Gm}{r}}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,水面下的光源S向水面A点发射一束光线,反射光线为c,折射光线分成a、b两束,则( )
如图所示,水面下的光源S向水面A点发射一束光线,反射光线为c,折射光线分成a、b两束,则( )| A. | 在水中a光的速度比b光的速度小 | |
| B. | 由于色散现象,经水面反射的光线c也可能分为两束 | |
| C. | 若保持入射点A位置不变,将入射光线顺时针旋转,则从水面上方观察,a光先消失 | |
| D. | 用同一双缝干涉实验装置分别以a、b光做实验,a光的干涉条纹间距大于b光的干涉条纹间距 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 全息照相主要是利用了光的衍射现象 | |
| B. | 泊松亮斑是光通过小圆盘发生衍射时形成的 | |
| C. | 单缝衍射形成的条纹宽度相同、亮度相同 | |
| D. | 光的衍射现象说明光具有粒子性 |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
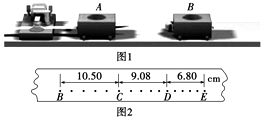
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 装好单摆,用力拉紧摆线,用米尺测出摆线长度,然后加上摆球的半径 | |
| B. | 用手托住摆球使其静止,用米尺直接测出悬点到球心的距离. | |
| C. | 让单摆自然下垂,用米尺测出摆线长度,然后加上摆球的半径 | |
| D. | 把单摆取下并放在桌面上,用米尺测出摆线长度,然后加上摆球的半径 |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
 图甲是“研究平抛运动”的实验装置图,为了完成实验,除了图甲中的仪器外,还必须图乙中选取的仪器有AD(填字母).以下是实验过程中的一些做法,其中合理的有AB(填字母).
图甲是“研究平抛运动”的实验装置图,为了完成实验,除了图甲中的仪器外,还必须图乙中选取的仪器有AD(填字母).以下是实验过程中的一些做法,其中合理的有AB(填字母).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com