
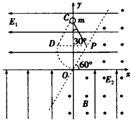
 如图所示,在xOy竖直平面内,长L的绝缘轻绳一端固定在第一象限的P点,另一端栓有一质量为m、带电荷量为+q的小球,OP距离也为L且与x轴的夹角为60°.在x轴上方有水平向左的匀强电场,场强大小为$\frac{\sqrt{3}mg}{3q}$,在x轴下方有竖直向上的匀强电场,场强大小为$\frac{mg}{q}$,过O和P两点的虚线右侧存在方向垂直xOy平面向外、磁感应强度为B的匀强磁场.小球置于y轴上的C点时,绳恰好伸直且与y轴夹角为30°,小球由静止释放后将沿CD方向做直线运动,到达D点时绳恰好绷紧,小球沿绳方向的分速度立即变为零,并以垂直于绳方向的分速度摆下,到达O点时将绳断开.不计空气阻力.求:
如图所示,在xOy竖直平面内,长L的绝缘轻绳一端固定在第一象限的P点,另一端栓有一质量为m、带电荷量为+q的小球,OP距离也为L且与x轴的夹角为60°.在x轴上方有水平向左的匀强电场,场强大小为$\frac{\sqrt{3}mg}{3q}$,在x轴下方有竖直向上的匀强电场,场强大小为$\frac{mg}{q}$,过O和P两点的虚线右侧存在方向垂直xOy平面向外、磁感应强度为B的匀强磁场.小球置于y轴上的C点时,绳恰好伸直且与y轴夹角为30°,小球由静止释放后将沿CD方向做直线运动,到达D点时绳恰好绷紧,小球沿绳方向的分速度立即变为零,并以垂直于绳方向的分速度摆下,到达O点时将绳断开.不计空气阻力.求:分析 (1)求出粒子受到的合力,然后由牛顿第二定律求出加速度;
(2)由运动学公式与动能定理可以求出粒子的速度;
(3)作出粒子的运动轨迹,牛顿第二定律、运动学公式、圆周运动周期公式求出粒子的运动时间.
解答 解:(1)如图所示,小球由静止释放时,所受重力和电场力的合力大小为:${F}_{合}=\sqrt{{{F}_{电}}^{2}+(mg)^{2}}$,
根据牛顿第二定律有:F合=ma,
解得:a=$\frac{2\sqrt{3}}{3}g$.
(2)设小球到达D点时的速度为v0,由运动学公式有:
${{v}_{0}}^{2}=2aL$,
垂直于绳方向的分速度为:v1=v0cos30°,
解得:v1=$\sqrt{\sqrt{3}gL}$.
从D点到O点的过程中,由动能定理得:
mgLcos30°-qE1L(1-sin30°)=$\frac{1}{2}m{v}^{2}-\frac{1}{2}m{{v}_{1}}^{2}$
解得:v=$\sqrt{\frac{5\sqrt{3}gL}{3}}$.
(3)因为qE2=mg,小球从O点以v垂直于虚线进入磁场将做匀速圆周运动, 根据牛顿第二定律有:$qvB=m\frac{{v}^{2}}{r}$,
根据牛顿第二定律有:$qvB=m\frac{{v}^{2}}{r}$,
得半径为:r=$\frac{mv}{qB}$,
周期为:T=$\frac{2πr}{v}=\frac{2πm}{qB}$.
小球进入磁场中运动$\frac{1}{2}$圆周后又垂直于虚线射出磁场,以v做匀速直线运动第一次打在x轴上,匀速直线运动的距离为:$d=2rtan60°=2\sqrt{3}r$,
${t}_{1}=\frac{T}{2}=\frac{πm}{qB}$,
${t}_{2}=\frac{d}{v}=\frac{2\sqrt{3}m}{qB}$,
小球再进入电场E1后,小球所受重力和电场力的合力垂直于v,小球做类平抛运动,
$\frac{\frac{1}{2}a{{t}_{3}}^{2}}{v{t}_{3}}=tan30°$,
解得:${t}_{3}=\sqrt{(\frac{5\sqrt{3}}{3})\frac{L}{g}}$.
则有:t=t1+t2+t3=$\frac{(π+2\sqrt{3})m}{qB}+\sqrt{(\frac{5\sqrt{3}}{3})\frac{L}{g}}$.
答:(1)小球刚释放瞬间的加速度大小a为$\frac{2\sqrt{3}}{3}g$;
(2)小球到达O点时的速度大小v为$\sqrt{\frac{5\sqrt{3}gL}{3}}$.;
(3)小球从O点开始到最终离开x轴的时间t为$\frac{(π+2\sqrt{3})m}{qB}+\sqrt{(\frac{5\sqrt{3}}{3})\frac{L}{g}}$.
点评 本题考查了粒子在电场与磁场中的运动,分析清楚粒子的运动过程、应用牛顿第二定律、运动学公式、动能定理、运动的合成与分解即可正确解题.


 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
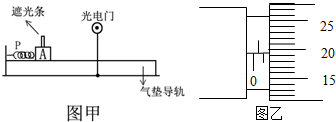
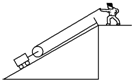 如图所示,建筑工人通过滑轮装置将一质量是100kg的料车沿30°角的斜面由底端匀速地拉到顶端,斜面长L是4m,若不计滑轮的质量和各处的摩擦力,g取10N/kg,求这一过程中:
如图所示,建筑工人通过滑轮装置将一质量是100kg的料车沿30°角的斜面由底端匀速地拉到顶端,斜面长L是4m,若不计滑轮的质量和各处的摩擦力,g取10N/kg,求这一过程中:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 紫外线照射到金属锌板表面时能够发生光电效应,则当增大紫外线的照射强度时,从锌板表面逸出的光电子的最大初动能也随之增大 | |
| B. | 质子和中子结合成新原子核一定有质量亏损,释放出能量 | |
| C. | 有10个放射性元素的原子核,当有5个原子核发生衰变所需的时间就是该放射性元素的半衰期 | |
| D. | 氢原子的核外电子由较高能级跃迁到较低能级时,要释放一定频率的光子,同时氢原子的电势能减小,电子的动能增大 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
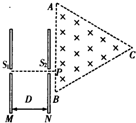 如图所示,M、N为中心开有小孔的平行板电容器的两极板,相距为D,其右侧有一边长为2a的正三角形区域,区域内有垂直纸面向里的匀强磁场,在极板M、N之间加上电压U后,M板电势高于N板电势.现有一带正电的粒子,质量为m、电荷量为q,其重力和初速度均忽略不计,粒子从极板M的中央小孔S1处射入电容器,穿过小孔S2后从距三角形A点$\sqrt{3}$a的P处垂直AB方向进入磁场,试求:
如图所示,M、N为中心开有小孔的平行板电容器的两极板,相距为D,其右侧有一边长为2a的正三角形区域,区域内有垂直纸面向里的匀强磁场,在极板M、N之间加上电压U后,M板电势高于N板电势.现有一带正电的粒子,质量为m、电荷量为q,其重力和初速度均忽略不计,粒子从极板M的中央小孔S1处射入电容器,穿过小孔S2后从距三角形A点$\sqrt{3}$a的P处垂直AB方向进入磁场,试求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 北京时间3月14日消息,2015短道速滑世锦赛于今晚在俄罗斯首都莫斯科展开了首个决赛日的争夺,在女子500米决赛中,接连有选手意外摔倒,由于短道速滑在比赛中很难超越对手,因而在比赛开始阶段每个选手都要以最大的加速度加速,在过弯道前超越对手,如果赛道的直道长度为L=30m,弯道半径为R=3m的圆弧形状,在弯道时,忽略冰面对选手的摩擦力,选手的运动视为匀速圆周运动,且地面对人的弹力沿身体方向,身体与冰面的夹角θ为30°,直线加速过程视为匀加速过程,加速度a=1m/s2,若比赛过程中选手没有减速过程,为保证比赛不出现意外情况,选手在直道上加速的最长距离为多少?(g取10m/s2)
北京时间3月14日消息,2015短道速滑世锦赛于今晚在俄罗斯首都莫斯科展开了首个决赛日的争夺,在女子500米决赛中,接连有选手意外摔倒,由于短道速滑在比赛中很难超越对手,因而在比赛开始阶段每个选手都要以最大的加速度加速,在过弯道前超越对手,如果赛道的直道长度为L=30m,弯道半径为R=3m的圆弧形状,在弯道时,忽略冰面对选手的摩擦力,选手的运动视为匀速圆周运动,且地面对人的弹力沿身体方向,身体与冰面的夹角θ为30°,直线加速过程视为匀加速过程,加速度a=1m/s2,若比赛过程中选手没有减速过程,为保证比赛不出现意外情况,选手在直道上加速的最长距离为多少?(g取10m/s2)查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图甲所示,在光滑水平面上的两小球A、B发生正碰,小球A的质量为m1=0.1kg.图乙为它们碰撞前后两个小球的s-t图象.由此可以判断( )
如图甲所示,在光滑水平面上的两小球A、B发生正碰,小球A的质量为m1=0.1kg.图乙为它们碰撞前后两个小球的s-t图象.由此可以判断( )| A. | 碰前小球B静止,小球A向右运动 | B. | 碰后小球A和B都向右运动 | ||
| C. | 小球B的质量为m2=0.2kg | D. | 小球B的质量为m2=0.3kg |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 近地卫星的环绕速度等于第一宇宙速度 | |
| B. | 所有同步卫星的质量可能不同,但绕行速度的大小是相同的 | |
| C. | 近地卫星或地球同步卫星上的物体,因“完全失重”,其运行加速度为零 | |
| D. | 地球同步卫星一定在地球赤道平面上的确定高度上运行 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com