
光滑水平面上有一质量为M=2 kg的足够长的木板,木板上最有端有一大小可忽略、质量为m=3kg的物块,物块与木板间的动摩擦因数![]() ,且最大静摩擦力等于滑动摩擦力。开始时物块和木板都静止,距木板左端L=2.4m处有一固定在水平面上的竖直弹性挡板P。现对物块施加一水平向左外力F=6N,若木板与挡板P发生撞击时间极短,并且搏击时无动能损失,物块始终未能与挡板相撞,求:
,且最大静摩擦力等于滑动摩擦力。开始时物块和木板都静止,距木板左端L=2.4m处有一固定在水平面上的竖直弹性挡板P。现对物块施加一水平向左外力F=6N,若木板与挡板P发生撞击时间极短,并且搏击时无动能损失,物块始终未能与挡板相撞,求:
(1)木板第一次撞击挡板P时的速度![]() 为多少?
为多少?
(2)木板从第一次撞击挡板P到运动至有端最远处所需的时间![]() 及此时物块距木板右端的距离X为多少?
及此时物块距木板右端的距离X为多少?
(3)木板与挡板P会发生多次撞击直至静止,而物块一直向左运动。每次木板与挡板p撞击前物块和木板都已相对静止,最后木板静止于挡板P处,求木板与物块都静止时物块距木板有端的距离X为多少?

(1)设木板靠最大静摩擦力或滑动摩擦力产生的加速度为am,则
am=![]() =6m/s2 ①
=6m/s2 ①
若木板与物块不发生相对运动,设共同加速度为a1,则
a1=![]() =1.2m/s 2 ②
=1.2m/s 2 ②
因a1<am,所以木板与物块靠静摩擦力一起以加速度a1运动 ③
根据运动学公式 ![]() =2a1L ④
=2a1L ④
解得 v=2.4m/s ⑤
(2)设木板第一次撞击挡板P后向右运动时,物块的加速度大小为a2,根据牛顿第二定律有 μmg—F=ma2 ⑥
解得 a2 =2m/s2 ⑦
因a2<am,所以在木板向右减速运动过程中,物块一直向左减速,木板速度减为0时,木块仍在向左运动。设木板第一次撞击挡板P后运动到右端最远处所需时间为t1,则
t1=![]() =0.4s ⑧
=0.4s ⑧
设木板左端距挡板P的距离为X1,则
![]() m ⑨
m ⑨
设物块相对地向左的位移为X2,则
X2=![]() t1—
t1—![]() a2t12 =0.8m ⑩
a2t12 =0.8m ⑩
此时物块距木板右端的距离X=X1+X2=1.28m ⑾
(3)木板最终静止于挡板P处,设物块距木板右端的距离为Xn,根据功能关系得
F(Xn+L)-μmgXn =0 ⑿
解得 Xn=2.4m ⒀
评分参考:第(1)问5分,①②③④⑤式各1分;第(2)问10分,其中⑥式2分,⑦式1分,⑧⑨⑩式各2分,⑾式1分;第(3)问5分,⑿式3分,⒀式2分。


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中物理 来源: 题型:
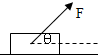 如图,在光滑水平面上有一质量为m的物体,在与水平方向成θ角的恒定拉力F作用下运动,则在时间t内( )
如图,在光滑水平面上有一质量为m的物体,在与水平方向成θ角的恒定拉力F作用下运动,则在时间t内( )| A、重力的冲量为0 | B、拉力F的冲量为Ft | C、拉力F的冲量为Ftcosθ | D、拉力F的冲量等于物体动量的变化量 |
查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,光滑水平面上有一质量M=1.0kg的小车,小车右端有一个质量m=0.90kg的滑块,滑块与小车左端的挡板之间用轻弹簧相连接,滑块与车面间的动摩擦因数μ=0.20,车和滑块一起以v1=10m/s的速度向右做匀速直线运动,此时弹簧为原长.一质量m0=0.10kg的子弹,以v0=50m/s的速度水平向左射入滑块而没有穿出,子弹射入滑块的时间极短.当弹簧压缩到最短时,弹簧被锁定(弹簧在弹性限度内),测得此时弹簧的压缩量d=0.50m,重力加速度g=10m/s2,求:
如图所示,光滑水平面上有一质量M=1.0kg的小车,小车右端有一个质量m=0.90kg的滑块,滑块与小车左端的挡板之间用轻弹簧相连接,滑块与车面间的动摩擦因数μ=0.20,车和滑块一起以v1=10m/s的速度向右做匀速直线运动,此时弹簧为原长.一质量m0=0.10kg的子弹,以v0=50m/s的速度水平向左射入滑块而没有穿出,子弹射入滑块的时间极短.当弹簧压缩到最短时,弹簧被锁定(弹簧在弹性限度内),测得此时弹簧的压缩量d=0.50m,重力加速度g=10m/s2,求:查看答案和解析>>
科目:高中物理 来源: 题型:
 光滑水平面上有一质量为M的木板,在木板的最左端有一质量为m的小滑块(可视为质点).小滑块与木板之间的动摩擦因数为μ.开始时它们都处于静止状态,某时刻给小滑块一瞬时冲量,使小滑块以初速度v0向右运动.经过一段时间小滑块与木板达到共同速度v,此时小滑块与木板最左端的距离为d,木板的位移为x,如图所示.下列关系式正确的是( )
光滑水平面上有一质量为M的木板,在木板的最左端有一质量为m的小滑块(可视为质点).小滑块与木板之间的动摩擦因数为μ.开始时它们都处于静止状态,某时刻给小滑块一瞬时冲量,使小滑块以初速度v0向右运动.经过一段时间小滑块与木板达到共同速度v,此时小滑块与木板最左端的距离为d,木板的位移为x,如图所示.下列关系式正确的是( )查看答案和解析>>
科目:高中物理 来源: 题型:
 光滑水平面上有一质量为M滑块,滑块的左侧是一光滑的
光滑水平面上有一质量为M滑块,滑块的左侧是一光滑的| 1 | 4 |
查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,光滑水平面上有一质量为M、长为L的长木板,其上有一质量为m的物块,它与长木板间的动摩擦因数为μ,开始时长木板与小物块均靠在与水平面垂直的左边固定挡板处以共同的速度v0向右运动,当长木板与右边固定竖直挡板碰撞后立即以大小相同的速率反向运动,且左右挡板之间的距离足够长.
如图所示,光滑水平面上有一质量为M、长为L的长木板,其上有一质量为m的物块,它与长木板间的动摩擦因数为μ,开始时长木板与小物块均靠在与水平面垂直的左边固定挡板处以共同的速度v0向右运动,当长木板与右边固定竖直挡板碰撞后立即以大小相同的速率反向运动,且左右挡板之间的距离足够长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com