
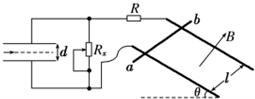
 如图所示,质量为M=2kg的导体棒ab,垂直放在相距为l=1m的平行光滑金属轨道上.导轨平面与水平面的夹角为θ=30°,并处于磁感应强度大小为B=2T、方向垂直与导轨平面向上的匀强磁场中,左侧是水平放置,间距为d=0.5m的平行金属板,R和Rx分别表示定值和滑动变阻器的阻值,定值电阻为R=3Ω,不计其他电阻.现将金属棒由静止释放,重力加速度为g=10m/s2,试求:
如图所示,质量为M=2kg的导体棒ab,垂直放在相距为l=1m的平行光滑金属轨道上.导轨平面与水平面的夹角为θ=30°,并处于磁感应强度大小为B=2T、方向垂直与导轨平面向上的匀强磁场中,左侧是水平放置,间距为d=0.5m的平行金属板,R和Rx分别表示定值和滑动变阻器的阻值,定值电阻为R=3Ω,不计其他电阻.现将金属棒由静止释放,重力加速度为g=10m/s2,试求:分析 (1)ab棒匀速下滑时,受力平衡,由平衡条件求电流I.由电磁感应定律求电动势E=BLv、闭合电路欧姆定律求速度v.
(2)由带电粒子的匀速通过电容器求电压,结合欧姆定律求出滑动变阻器阻值.
解答 解:(1)ab匀速下滑处于平衡状态,由平衡条件得:Mgsinθ=BIl,
解得,通过棒的电流为:I=$\frac{Mgsinθ}{Bl}$=$\frac{2×10sin30°}{2×1}$=5A;
感应电流:I=$\frac{Blv}{R+{R}_{x}}$,解得:v=$\frac{I(R+{R}_{X})}{Bl}$=$\frac{5×(3+3)}{2×1}$=15m/s;
(2)微粒在板间做匀速直线运动,
由平衡条件得:q$\frac{U}{d}$=mg,
由欧姆定律得:Rx=$\frac{U}{I}$,
解得:Rx=$\frac{mBdl}{Mqsinθ}$=$\frac{3×1{0}^{-4}×2×0.5×1}{2×5×1{0}^{-5}sin30°}$=12Ω;
答:(1)通过棒的电流I为5A,棒的速率v为15m/s;
(2)此时的Rx为12Ω.
点评 本题是导体在导轨上滑动和磁流体发电机的综合类型,从力和能量两个角度研究,关键要掌握法拉第定律、欧姆定律等等基本规律,并能正确运用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中物理 来源: 题型:计算题
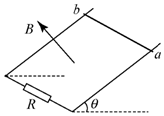 如图所示,两平行金属导轨电阻不计,相距L=1m,导轨平面与水平面的夹角θ=37°,导轨的下端连接一个电阻R.匀强磁场的方向垂直于导轨平面向上,磁感应强度为B=0.4T.质量为0.2kg、电阻不计的金属棒垂直放在两导轨上且保持良好接触,金属棒和导轨间的动摩擦因数为μ=0.25.金属棒沿导轨由静止开始下滑,当金属棒下滑的速度达到稳定时,其速度的大小为10m/s.g取10m/s2,已知sin37°=0.6,cos37°=0.8,求:
如图所示,两平行金属导轨电阻不计,相距L=1m,导轨平面与水平面的夹角θ=37°,导轨的下端连接一个电阻R.匀强磁场的方向垂直于导轨平面向上,磁感应强度为B=0.4T.质量为0.2kg、电阻不计的金属棒垂直放在两导轨上且保持良好接触,金属棒和导轨间的动摩擦因数为μ=0.25.金属棒沿导轨由静止开始下滑,当金属棒下滑的速度达到稳定时,其速度的大小为10m/s.g取10m/s2,已知sin37°=0.6,cos37°=0.8,求:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | b星公转的周期为$\frac{l-△r}{l+△r}$T | B. | a、b两颗星的半径之比为$\frac{l}{l-△r}$ | ||
| C. | a星公转的线速度大小为$\frac{π(l+△r)}{T}$ | D. | a、b两颗星的质量之比为$\frac{l-△r}{l+△r}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
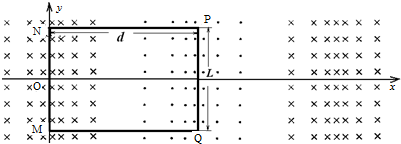
 如图所示,MN、PQ为相距L的光滑平行的金属导轨,导轨平面与水平面夹角为θ,导轨处于磁感应强度为B、方向垂直于导轨平面向上的匀强磁场中,在两导轨间接有一电阻为R的定值电阻,质量为m的导体棒从ab处由静止开始下滑,加速运动到位置cd处时棒的速度大小为v,此过程中通过电阻的电量为q,除R外,回路其余电阻不计,求:
如图所示,MN、PQ为相距L的光滑平行的金属导轨,导轨平面与水平面夹角为θ,导轨处于磁感应强度为B、方向垂直于导轨平面向上的匀强磁场中,在两导轨间接有一电阻为R的定值电阻,质量为m的导体棒从ab处由静止开始下滑,加速运动到位置cd处时棒的速度大小为v,此过程中通过电阻的电量为q,除R外,回路其余电阻不计,求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
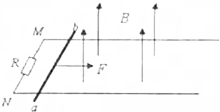 两根足够长且平行的光滑金属导轨M、N水平固定放置,电阻忽略不计,两导轨左端连接有一阻值为R的电阻,导轨间存在竖直向上的匀强磁场,将一质量为m的导体棒ab放置在两导轨上,并始终保持与导轨垂直接触,导体棒接入导轨间部分的电阻值为r,现出现与导体棒施加一大小恒为F的水平向右拉力,使之从静止开始运动,如图所示,在导体棒ab运动了x的距离时,测得其速度为v,重力加速度为g,试求:
两根足够长且平行的光滑金属导轨M、N水平固定放置,电阻忽略不计,两导轨左端连接有一阻值为R的电阻,导轨间存在竖直向上的匀强磁场,将一质量为m的导体棒ab放置在两导轨上,并始终保持与导轨垂直接触,导体棒接入导轨间部分的电阻值为r,现出现与导体棒施加一大小恒为F的水平向右拉力,使之从静止开始运动,如图所示,在导体棒ab运动了x的距离时,测得其速度为v,重力加速度为g,试求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 反射光线也转过θ角 | |
| B. | 反射光线转过2θ角 | |
| C. | 入射角增大2θ角 | |
| D. | 反射光线与入射光线的夹角增大θ角 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
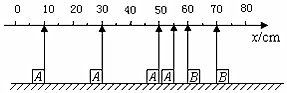
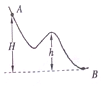 某游客领着孩子爬山时,不小心将手中的皮球滑落,皮球从A点滚到了山脚下的B点,高度标记如图所示,皮球从A运动到B点的过程中( )
某游客领着孩子爬山时,不小心将手中的皮球滑落,皮球从A点滚到了山脚下的B点,高度标记如图所示,皮球从A运动到B点的过程中( )| A. | 运动轨迹未知,无法求出重力做的功 | |
| B. | 阻力大小未知,无法求出重力做的功 | |
| C. | 重力做功mg(H-h) | |
| D. | 重力做功mgH |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com