
 如图所示,在坐标系xoy中,过原点的直线OC与x轴正向的夹角φ=120°,在OC右侧有一匀强电场:在第二、三象限内有一匀强磁场,其上边界与电场边界重叠、右边界为y轴、左边界为图中平行于y轴的虚线,磁场的磁感应强度大小为B,方向垂直纸面向里.一带正电荷q、质量为m的粒子以某一速度自磁场左边界上的A点沿x轴正方向射入磁场区域,并从O点射出,粒子射出磁场的速度方向与x轴的夹角θ=30°,大小为v,粒子在磁场中的运动轨迹为纸面内的一段圆弧,且弧的半径为磁场左右边界间距的两倍.粒子进入电场后,在电场力的作用下又由O点返回磁场区域,经过一段时间后再次离开磁场.已知粒子从A点射入到第二次离开磁场所用的时间恰好等于粒子在磁场中做圆周运动的周期.忽略重力的影响.求:
如图所示,在坐标系xoy中,过原点的直线OC与x轴正向的夹角φ=120°,在OC右侧有一匀强电场:在第二、三象限内有一匀强磁场,其上边界与电场边界重叠、右边界为y轴、左边界为图中平行于y轴的虚线,磁场的磁感应强度大小为B,方向垂直纸面向里.一带正电荷q、质量为m的粒子以某一速度自磁场左边界上的A点沿x轴正方向射入磁场区域,并从O点射出,粒子射出磁场的速度方向与x轴的夹角θ=30°,大小为v,粒子在磁场中的运动轨迹为纸面内的一段圆弧,且弧的半径为磁场左右边界间距的两倍.粒子进入电场后,在电场力的作用下又由O点返回磁场区域,经过一段时间后再次离开磁场.已知粒子从A点射入到第二次离开磁场所用的时间恰好等于粒子在磁场中做圆周运动的周期.忽略重力的影响.求:分析 (1)结合运动的轨迹图象,判断出圆周运动的圆心即两虚线的交点,再根据洛伦兹力提供向心力,粒子的速度和A到y轴的距离;
(2)粒子进入电场后,在电场力的作用下又由O点返回磁场区域说明电场力的方向一定与运动的方向相反,则电场方向必与v相反;根据时间关系求出粒子在电场中运动的时间,进而求出电场的强度和方向;
(3)粒子出磁场后到进入电场是匀速直线运动,根据轨迹图象,就可以求出从第二次离开磁场到再次进入电场所用的时间.
解答 解:(1)设磁场左右边界间距为d,由几何关系知:OO′=2d,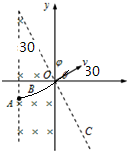
粒子第一次进入磁场的运动轨迹的圆心为O′,有:$\overline{AD}=R(1-cos{30^0})$,
洛伦兹力提供向心力,由牛顿第二定律得:$qBv=m\frac{v^2}{R}$,
解得:$\overline{AD}=\frac{mv}{qB}(1-\frac{{\sqrt{3}}}{2})$;
(2)粒子在磁场中做圆周运动的周期:$T=\frac{2πm}{qB}$,
粒子第一次在磁场中运动时间为t1,有:t1=$\frac{30°}{360°}$T=$\frac{1}{12}$T,
依题意,匀强电场的方向与x轴正向夹角应为150°.
由几何关系知,粒子再次从O点进入磁场的速度方向与磁场右边界夹角为60°.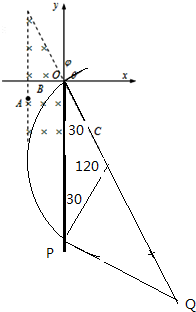
粒子第二次在磁场运动的圆弧的圆心O″必定在直线OC上,且∠OO″P=120°
粒子第二次在磁场中运动时间为t2,有:${t_1}=\frac{T}{3}$
粒子在电场中运动时间为t3,依题意有:t3=T-(t1+t2)
粒子在电场中有:-v=v-at3,
由牛顿第二定律的:qE=ma,
解得:E=$\frac{12Bv}{7π}$;
(3)粒子自P射出后沿直线运动,由P′再次进入电场,由几何关系有:∠O″P′P=30°
三角形OPP′为等腰三角形,粒子在P、P′运动时间为t4,有:${t_4}=\frac{{\overline{P{P^/}}}}{v}$
由几何关系得:$\overline{OP}=\sqrt{3}R$,
解得:t4=$\frac{\sqrt{3}m}{qB}$;
答:(1)A点到x轴的距离为(1-$\frac{\sqrt{3}}{2}$)$\frac{mv}{qB}$;
(2)匀强电场的大小为$\frac{12Bv}{7π}$,方向:与v的方向相反;
(3)粒子从第二次离开磁场到再次进入电场时所用的时间为$\frac{\sqrt{3}m}{qB}$.
点评 带电粒子在磁场中 的运动,正确地画出运动的轨迹是解题的关键,象该题需要两次画出不同的轨迹.题目的难度较大.


科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,某轻杆一端固定一质量为m的小球,以另一端O为圆心,使小球在竖直平面内做半径为R的圆周运动,以下说法中正确的是( )
如图所示,某轻杆一端固定一质量为m的小球,以另一端O为圆心,使小球在竖直平面内做半径为R的圆周运动,以下说法中正确的是( )| A. | 小球过最高点时,杆所受的弹力可以为零 | |
| B. | 小球过最高点时,最小速度为$\sqrt{gR}$ | |
| C. | 小球过最高点时,杆对球的作用力可以与球所受重力方向相反,此时重力一定大于或等于杆对球的作用力 | |
| D. | 小球过最低点时,杆对球的作用力可能与小球所受重力方向相同 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,沿x轴正方向传播的一列简谐横波在某时刻的波形图为一正弦曲线,若波速为200m/s,则下列说法中正确的是( )
如图所示,沿x轴正方向传播的一列简谐横波在某时刻的波形图为一正弦曲线,若波速为200m/s,则下列说法中正确的是( )| A. | 从图示时刻开始,质点b的加速度将增大 | |
| B. | 图示时刻,质点b的振动方向沿y轴正方向 | |
| C. | 若此波遇到另一列波并发生稳定干涉现象,则另一列波的频率为50Hz | |
| D. | 质点A在任意的1s内所通过的路程都是0.8m |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图是氢原子的能级图.已知基态氢原子的能量为E1=-13.6eV.一群氢原子从n=3的能量状态自发地向低能级跃迁的过程中,最多可以辐射出几种频率的光子?有哪几种光线可以使极限频率为8.07×1014Hz的锌板发生光电效应?产生的光电子最大初动能是多少电子伏?
如图是氢原子的能级图.已知基态氢原子的能量为E1=-13.6eV.一群氢原子从n=3的能量状态自发地向低能级跃迁的过程中,最多可以辐射出几种频率的光子?有哪几种光线可以使极限频率为8.07×1014Hz的锌板发生光电效应?产生的光电子最大初动能是多少电子伏?查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | $\frac{4{π}^{2}{r}^{3}}{G{T}^{2}}$ | B. | $\frac{4{π}^{2}{r}^{2}}{G{T}^{2}}$ | C. | $\frac{4{π}^{2}r}{G{T}^{2}}$ | D. | $\frac{4{π}^{2}{r}^{3}}{GT}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题

| A. | a1、b1两点的场强相同,电势相同 | B. | c1、d1两点的场强相同,电势相同 | ||
| C. | a2、b2两点的场强相同,电势相同 | D. | c2、d2两点的场强相同,电势相同 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com