
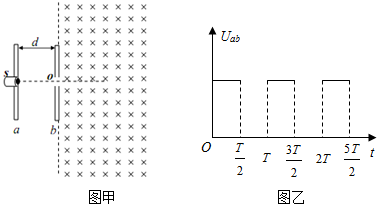
分析 (1)粒子进入电场后做加速运动,由牛顿第二定律和运动学公式求解速度大小
(2)进入磁场后做匀速圆周运动,由洛伦兹力充当向心力得半径,根据周期公式求时间
(3)进入磁场的最小速度对应粒子匀速运动时间最长,则加速时间最短,速度最小,画出粒子运动图象由运动学公式求解面积.
解答 解:(1)粒子进入电场后做加速运动,时间为t,加速度为a,O点速度为V1
由牛顿第二定律知:a=$\frac{qE}{m}=\frac{q{U}_{0}}{md}$
根据运动学公式:d=$\frac{1}{2}a{t}^{2}$,t=$\sqrt{\frac{2d}{a}}=\frac{T}{2}$
粒子在0.5T时刻出电场
所以V1=at=$\sqrt{\frac{2q{U}_{0}}{m}}$
(2)进入磁场后做匀速圆周运动,由洛伦兹力充当向心力得:
${r}_{1}=\frac{m{V}_{1}}{qB}=d$
运动时间${t}_{2}=\frac{{T}_{轨}}{2}=\frac{2πm}{qB}$×$\frac{1}{2}$=$πd\sqrt{\frac{m}{2q{U}_{0}}}$
(3)进入磁场的最小速度为V2
粒子匀速运动时间最长,则加速时间最短,速度最小
所以最长时间为0.5T,运动位移${S}_{2}={V}_{2}×\frac{T}{2}$
在ab间加速运动位移${S}_{1}=\frac{{V}_{2}^{2}-0}{2a}$
根据题意得d=S1-S2
解得:${V}_{2}=(2-\sqrt{2})\sqrt{\frac{q{U}_{0}}{m}}$
在磁场中的半径${r}_{2}=\frac{m{V}_{2}}{qB}=(\sqrt{2}-1)d$
运动区域如图
面积S=$\frac{1}{2}(π{r}_{1}^{2}-π{r}_{2}^{2})$=$(\sqrt{2}-1)π{d}^{2}$
答:(1)t=0时刻进入加速电场的粒子进入磁场的速度大小$\sqrt{\frac{2q{U}_{0}}{m}}$;
(2)t=0时刻进入加速电场的粒子在磁场中运动轨道半径d和运动时间$πd\sqrt{\frac{m}{2q{U}_{0}}}$
(3)该区域面积大小$(\sqrt{2}-1)π{d}^{2}$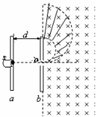
点评 本题中粒子先在电场中做加速直线运动,后做匀速圆周运动.由运动学公式或动能定理可求得末速度及时间;而在磁场中做圆周运动,确定圆心和半径为解题的关键


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中物理 来源: 题型:解答题
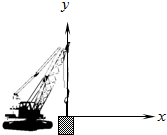 如图所示,吊车以恒定速度v沿x轴正方向匀速前进,同时以恒定的加速度a由静止匀加速吊起重物(沿y轴正方向),请大致画出重物运动的轨迹.经过t时间,重物的速度大小为$\sqrt{{v^2}+{a^2}{t^2}}$.
如图所示,吊车以恒定速度v沿x轴正方向匀速前进,同时以恒定的加速度a由静止匀加速吊起重物(沿y轴正方向),请大致画出重物运动的轨迹.经过t时间,重物的速度大小为$\sqrt{{v^2}+{a^2}{t^2}}$.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
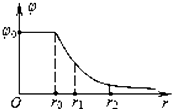 若取无穷远处为零电势,某一直线上各点的电势φ分布规律可用图中曲线表示,r表示该直线上某点到原点O的距离,r1、r2分别是该直线上A、B两点离原点O的距离.下列说法中正确的是( )
若取无穷远处为零电势,某一直线上各点的电势φ分布规律可用图中曲线表示,r表示该直线上某点到原点O的距离,r1、r2分别是该直线上A、B两点离原点O的距离.下列说法中正确的是( )| A. | O-r0这个区域的电场强度最大 | |
| B. | A点的电场强度可能等于B点的电场强度 | |
| C. | 若r2-r1=r1-r0,则φA-φB=φ0-φA | |
| D. | 将α粒子从A点移到B点,电场力做正功 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 一切物体的“自然运动”都是速度不变的运动--静止或者匀速直线运动 | |
| B. | 作用在物体上的力,是使物体做“受迫运动”即变速运动的原因 | |
| C. | 竖直向上抛出的物体,受到了重力,却没有立即反向运动,而是继续向上运动一段距离后才反向运动,是由于物体具有惯性 | |
| D. | 可绕竖直轴转动的水平圆桌转得太快时,放在桌面上的盘子会向桌子边缘滑去,这是由于“盘子受到的向外的力”超过了“桌面给盘子的摩擦力”导致的 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 现在低碳环保问题已引起广大人民群众的普遍关注,深圳市民林先生自主研发出一种磁悬浮风力发电机,其发电原理可以简化为:一个矩形线圈绕在其平面内并且垂直于匀强磁场的轴做匀速转动而产生感应电动势,产生的感应电动势图象如图所示,并且接在原副线圈匝数比为$\frac{{n}_{1}}{{n}_{2}}$=$\frac{1}{5}$的理想变压器原线圈两端,则( )
现在低碳环保问题已引起广大人民群众的普遍关注,深圳市民林先生自主研发出一种磁悬浮风力发电机,其发电原理可以简化为:一个矩形线圈绕在其平面内并且垂直于匀强磁场的轴做匀速转动而产生感应电动势,产生的感应电动势图象如图所示,并且接在原副线圈匝数比为$\frac{{n}_{1}}{{n}_{2}}$=$\frac{1}{5}$的理想变压器原线圈两端,则( )| A. | 变压器副线圈两端电压的有效值为U2=110 V | |
| B. | 感应电动势的瞬时值表达式为e=22$\sqrt{2}$sin 10πt(V) | |
| C. | t=0.005 s时穿过线圈平面的磁通量最大 | |
| D. | t=0.005 s时线圈平面和磁场方向平行 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题

| A. | 在0~t1时间内,通过线圈的电荷量为0.5C | |
| B. | 线圈匀速运动的速度大小为8m/s | |
| C. | 线圈的长度为1m | |
| D. | 0~t3时间内,线圈产生的热量为1.8J |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
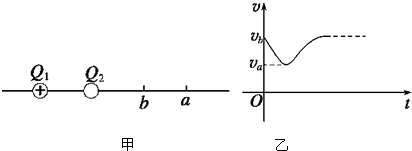
| A. | Q2带正电 | |
| B. | a、b两点的电势φa>φb | |
| C. | a、b两点电场强度Ea>Eb | |
| D. | 试探电荷从b到a的过程中电势能减小 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com