
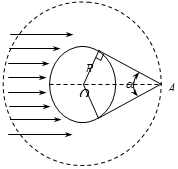
 宇宙飞船以周期为T绕地球作圆周运动时,由于地球遮挡阳光,会经历“日全食”过程,如图所示.已知地球的半径为R,引力常量为G,地球自转周期为T0,太阳光可看作平行光,宇航员在轨道上A点测出的张角为α,则( )
宇宙飞船以周期为T绕地球作圆周运动时,由于地球遮挡阳光,会经历“日全食”过程,如图所示.已知地球的半径为R,引力常量为G,地球自转周期为T0,太阳光可看作平行光,宇航员在轨道上A点测出的张角为α,则( )| A. | 飞船绕地球运动的线速度为$\frac{2πR}{Tsin(\frac{α}{2})}$ | |
| B. | 一天内飞船经历“日全食”的次数为$\frac{{T}_{0}}{T}$ | |
| C. | 飞船每次“日全食”过程的时间为$\frac{αT}{π}$ | |
| D. | 地球密度为$\frac{3π}{G{T}^{2}}$ |
分析 宇宙飞船绕地球做匀速圆周运动,由飞船的周期及半径可求出飞船的线速度;同时由万有引力提供向心力的表达式,可列出周期与半径及角度α的关系.当飞船进入地球的影子后出现“日全食”到离开阴影后结束,所以算出在阴影里转动的角度,即可求出发生一次“日全食”的时间;由地球的自转时间与宇宙飞船的转动周期,可求出一天内飞船发生“日全食”的次数.
解答 解:A、飞船绕地球匀速圆周运动,
所以线速度为v=$\frac{2πr}{T}$
又由几何关系知$sin\frac{α}{2}=\frac{R}{r}$
所以 $v=\frac{2πR}{Tsin\frac{α}{2}}$ 故A正确;
B、地球自转一圈时间为To,飞船绕地球一圈时间为T,飞船绕一圈会有一次日全食,所以每过时间T就有一次日全食,得一天内飞船经历“日全食”的次数为$\frac{{T}_{0}^{\;}}{T}$. 故B正确;
C、由几何关系,飞船每次“日全食”过程的时间内飞船转过α角,所需的时间为t=$\frac{π-α}{2π}T$;故C错误;
D、万有引力提供向心力则
所以:$G\frac{Mm}{{r}_{\;}^{2}}=m\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}r$
得$M=\frac{4{π}_{\;}^{2}{r}_{\;}^{3}}{G{T}_{\;}^{2}}$=$\frac{4{π}_{\;}^{2}{R}_{\;}^{3}}{G{T}_{\;}^{2}si{n}_{\;}^{3}\frac{α}{2}}$
所以:$ρ=\frac{M}{V}=\frac{\frac{4{π}_{\;}^{2}{R}_{\;}^{3}}{G{T}_{\;}^{2}si{n}_{\;}^{3}\frac{α}{2}}}{\frac{4π{R}_{\;}^{3}}{3}}$=$\frac{3π}{G{T}_{\;}^{2}si{n}_{\;}^{3}\frac{α}{2}}$,故D错误;
故选:AB.
点评 掌握匀速圆周运动中线速度、角速度及半径的关系,同时理解万有引力定律,并利用几何关系得出转动的角度.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:高中物理 来源: 题型:选择题
 我们的家乡雅安是中国优秀旅游城市.“马踏飞燕”是“中国优秀旅游城市”标志.如图所示,飞奔的骏马三足腾空,只用一只蹄就能稳稳地踏在飞翔的燕子上,是因为( )
我们的家乡雅安是中国优秀旅游城市.“马踏飞燕”是“中国优秀旅游城市”标志.如图所示,飞奔的骏马三足腾空,只用一只蹄就能稳稳地踏在飞翔的燕子上,是因为( )| A. | 马跑得快的缘故 | |
| B. | 马蹄大的缘故 | |
| C. | 马的重心在飞燕上 | |
| D. | 马的重心位置和飞燕在一条竖直线上 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 在世界机器人大赛上.中科大“蓝鹰”队机器人“可佳”现要执行一项任务.给它设定了如下动作程序:机器人在平面内.由点(0,0)出发.沿直线运动到点(3,1).然后又由点(3,1)沿直线运动到点(1,4).然后又由点(1,4)沿直线运动到点(5,5).然后又由点(5,5)沿直线运动到点(2,2).该个过程中机器人所用时间是2$\sqrt{2}$s.则下列说法正确的是( )
在世界机器人大赛上.中科大“蓝鹰”队机器人“可佳”现要执行一项任务.给它设定了如下动作程序:机器人在平面内.由点(0,0)出发.沿直线运动到点(3,1).然后又由点(3,1)沿直线运动到点(1,4).然后又由点(1,4)沿直线运动到点(5,5).然后又由点(5,5)沿直线运动到点(2,2).该个过程中机器人所用时间是2$\sqrt{2}$s.则下列说法正确的是( )| A. | 机器人的运动轨迹是一条直线 | |
| B. | 机器人不会两次通过同一点 | |
| C. | 整个过程中机器人的位移大小为2$\sqrt{2}$m | |
| D. | 整个过程中机器人的平均速率为1m/s |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
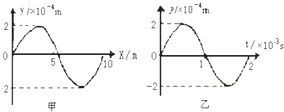
| A. | 甲图是振动图象,此列波的波速为2×104m/s | |
| B. | 甲图是波动图象,此列波的波速为2×102m/s | |
| C. | 乙图是波动图象,此列波的波速为5×102m/s | |
| D. | 乙图是振动图象,此列波的波速为5×103m/s |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
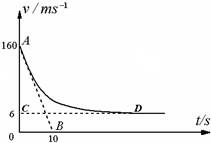 “神舟”六号飞船完成了预定空间科学和技术试验任务后,返回舱于2005年10月17日4时11分开始从太空向地球表面按预定轨道返回.在离地l0km的高度返回舱打开阻力降落伞减速下降,返回舱在这一过程中所受空气阻力与速度的平方成正比,比例系数(空气阻力系数)为k.已知返回舱的总质量M=3000kg,所受空气浮力恒定不变,且认为竖直降落.从某时刻起开始计时,返回舱的运动v-t图象如图中的AD曲线所示,图中AB是曲线在A点的切线,切线交于横轴于B点的坐标为( 10,0 ),CD是AD的渐近线,亦是平行于横轴的直线,交纵轴于C点,C点的坐标为( 0,6 ).请解决下列问题:(取g=10m/s2)
“神舟”六号飞船完成了预定空间科学和技术试验任务后,返回舱于2005年10月17日4时11分开始从太空向地球表面按预定轨道返回.在离地l0km的高度返回舱打开阻力降落伞减速下降,返回舱在这一过程中所受空气阻力与速度的平方成正比,比例系数(空气阻力系数)为k.已知返回舱的总质量M=3000kg,所受空气浮力恒定不变,且认为竖直降落.从某时刻起开始计时,返回舱的运动v-t图象如图中的AD曲线所示,图中AB是曲线在A点的切线,切线交于横轴于B点的坐标为( 10,0 ),CD是AD的渐近线,亦是平行于横轴的直线,交纵轴于C点,C点的坐标为( 0,6 ).请解决下列问题:(取g=10m/s2)查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,质量为4kg的物体与水平地面的动摩擦因数为μ=0.20,现对物体作用一向右与水平方向成37°、大小为20N的拉力F,使之向右做匀加速运动,求:(g=10m/s2)
如图所示,质量为4kg的物体与水平地面的动摩擦因数为μ=0.20,现对物体作用一向右与水平方向成37°、大小为20N的拉力F,使之向右做匀加速运动,求:(g=10m/s2)查看答案和解析>>
科目:高中物理 来源: 题型:计算题
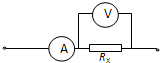 如图所示是用电压表
如图所示是用电压表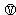 和电流表
和电流表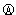 测电阻的一种连接方法,Rx为待测电阻.如果
测电阻的一种连接方法,Rx为待测电阻.如果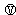 的读数是4.50V,
的读数是4.50V,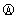 的读数是25.0mA,电压表的电阻是1.0kΩ,求:
的读数是25.0mA,电压表的电阻是1.0kΩ,求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 刀的刃部一般比较薄,刀刃对木块产生的力F可分解为如图所示的两个相同的分力F1,F2,下列说法正确的是( )
刀的刃部一般比较薄,刀刃对木块产生的力F可分解为如图所示的两个相同的分力F1,F2,下列说法正确的是( )| A. | 同样大小的F作用下,刃部越薄,F1与F2越大 | |
| B. | 同样大小的F作用下,刃部越薄,F1与F2越小 | |
| C. | F越大,F1与F2越小 | |
| D. | F分解成F1与F2时不遵守平行四边形定则 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com