
 ��ͼ����ʾ��һֻ������S=0.11m2������Ϊ100�ѵıպ���Ȧ����ƽ������Ȧ���ߵ���ǿ�ų��У���Ȧ���ܵ���R=1.1��������ǿ�ų��ĴŸ�Ӧǿ��B��ʱ��t�仯�Ĺ�����ͼ����ʾ����
��ͼ����ʾ��һֻ������S=0.11m2������Ϊ100�ѵıպ���Ȧ����ƽ������Ȧ���ߵ���ǿ�ų��У���Ȧ���ܵ���R=1.1��������ǿ�ų��ĴŸ�Ӧǿ��B��ʱ��t�仯�Ĺ�����ͼ����ʾ�������� ��1�������ȷ���Ÿ�Ӧǿ��B�ı仯��$\frac{��B}{��t}$�����ݷ����ڵ�Ÿ�Ӧ���������Ӧ�綯�ƣ�
��2���ɷ����ڵ�Ÿ�Ӧ���ɡ�ŷķ���ɺ͵����Ķ���ʽI=$\frac{q}{t}$�������������
��3����0��0.3s���ɽ������ɷֱ����������������⣮
��� �⣺��1����t=0��t=0.2 sʱ���ڣ���ͼ�ҿ�֪��$\frac{��{B}_{1}^{\;}}{��{t}_{1}^{\;}}$=0.5 T/s
�ɷ����ڵ�Ÿ�Ӧ���ɿ�֪��·�еĵ綯��E1=n$\frac{��{B}_{1}^{\;}}{��{t}_{1}^{\;}}S$=100��0.5��0.11�T5.5 V��
��t=0.2 s��t=0.3 sʱ���ڣ���ͼ��֪��$\frac{��{B}_{2}^{\;}}{��{t}_{2}^{\;}}$=1 T/s
�ɷ����ڵ�Ÿ�Ӧ���ɣ���֪��·�еĵ綯��E2=n$\frac{��{B}_{2}^{\;}}{��{t}_{2}^{\;}}S$�T100��1��0.11=11 V����
��2����t=0��t=0.2 sʱ���ڣ���·�еĵ���I1�T$\frac{{E}_{1}^{\;}}{R}=\frac{5.5}{1.1}$=5 A��
���ʱ����ͨ����Ȧ�ĵ����q1=I1��t1=5��0.2=1 C��
��t=0.2 s��t=0.3 sʱ���ڣ���·�еĵ��� I2�T$\frac{11}{1.1}$=10 A��
���ʱ����ͨ����Ȧ�ĵ����q2=I2��t2=10��0.1=1 C��
��t=0��t=0.3 sʱ���ڣ�ͨ������Ȧ����һ�������ĵ����q=q1+q2=2 C����
��3����t=0��t=0.2 sʱ���ڣ���·�в���������Q1=${I}_{1}^{2}$R${t}_{1}^{\;}$=${5}_{\;}^{2}��1.1��0.2$=5.5 J��
��t=0.2 s��t=0.3 sʱ���ڣ���·�в���������ΪQ2=${I}_{2}^{2}$Rt2=$1{0}_{\;}^{2}��1.1��0.1$=11 J��
��Q=Q1+Q2=16.5 J����
�𣺣�1����0��0.2sʱ�����Լ���0.2s��0.3sʱ���ڻ�·�еĸ�Ӧ�綯��Ϊ11V��
��2����0��0.3sʱ���ڣ�ͨ������Ȧ����һ�������ĵ����qΪ2C��
��3����0��0.3s����Ȧ�в����Ľ�����QΪ16.5J��
���� �����Ƿ����ڵ�Ÿ�Ӧ���ɡ�ŷķ���ɡ��������ɺ���ζ��ɵ�֪ʶ���ۺ�Ӧ�ã���Щ���ǵ�Ÿ�Ӧ�������صĻ������ɣ�Ҫ�������գ�������ȷӦ�ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 ��ͼ��ʾ��С��Ӹߴ����䵽��ֱ���õ��ᵯ���ϣ��ڵ���ѹ������̵����������У����й�����������������ȷ��Ӧ�ǣ�������
��ͼ��ʾ��С��Ӹߴ����䵽��ֱ���õ��ᵯ���ϣ��ڵ���ѹ������̵����������У����й�����������������ȷ��Ӧ�ǣ�������| A�� | С��սӴ�����ʱ������� | |
| B�� | С��սӴ����ɺ�����������С | |
| C�� | �ڵ���ѹ�������ʱС���������ܺͶ���֮����� | |
| D�� | ������ڵ���ѹ�������ʱС���������ܺ͵��ɵ�������֮����� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ʵ����
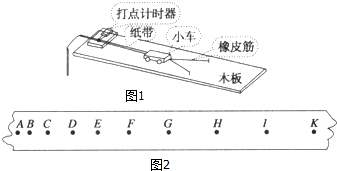
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
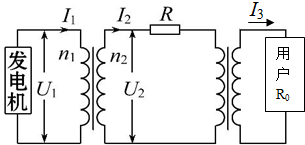 ��ͼΪijС��ˮ��վ�ĵ�������ʾ��ͼ�������ͨ����ѹ��ѹ��T1�ͽ�ѹ��ѹ��T2���û����磮��֪������ܵ���R=10������ѹ��ѹ����T1ԭ������Ȧ����֮��Ϊ1��5����ѹ��ѹ����T2ԭ������Ȧ����֮��Ϊ4��1������Ȧ�봿������ɱպϵ�·���õ�������R0=11������T1��T2��Ϊ�����ѹ����T2�ĸ���Ȧ���˵�ѹ����ʽΪu=220$\sqrt{2}$sin100��t V����
��ͼΪijС��ˮ��վ�ĵ�������ʾ��ͼ�������ͨ����ѹ��ѹ��T1�ͽ�ѹ��ѹ��T2���û����磮��֪������ܵ���R=10������ѹ��ѹ����T1ԭ������Ȧ����֮��Ϊ1��5����ѹ��ѹ����T2ԭ������Ȧ����֮��Ϊ4��1������Ȧ�봿������ɱպϵ�·���õ�������R0=11������T1��T2��Ϊ�����ѹ����T2�ĸ���Ȧ���˵�ѹ����ʽΪu=220$\sqrt{2}$sin100��t V�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ����õ�����ƾ����λ�ö����е������������� | |
| B�� | ���������˶������е������������� | |
| C�� | �������ܵı���ʽ�ǣ�Ep=mgh�����ܵı���ʽ�ǣ�${E_k}=\frac{1}{2}m{v^2}$ | |
| D�� | ������������������ʹ����������������� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | �Ȼ��ǰ�����ת��Ϊ��е�ܵ�װ�� | |
| B�� | �Ȼ��ǰѻ�е��ת��Ϊ���ܵ�װ�� | |
| C�� | ֻҪ����ȼ�����Ͻ��и��£����������������ȫ��ת��Ϊ��е�� | |
| D�� | ��ʹû��©����Ҳû��Ħ������ȼ��Ҳ���ܰ�����ȫ��ת��Ϊ��е�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
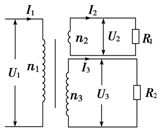 ��ͼ��ʾ��һ�����ѹ����һ��������Ȧ�������μ���Ȧ��ɣ����˱�ѹ������ʱ�������ʹμ���Ȧ����������������ѹ����ͼ�б���������м����ϵʽ����ȷ���ǣ�������
��ͼ��ʾ��һ�����ѹ����һ��������Ȧ�������μ���Ȧ��ɣ����˱�ѹ������ʱ�������ʹμ���Ȧ����������������ѹ����ͼ�б���������м����ϵʽ����ȷ���ǣ�������| A�� | $\frac{{U}_{1}}{{U}_{2}}$=$\frac{{n}_{1}}{{n}_{2}}$��$\frac{{U}_{1}}{{U}_{3}}$=$\frac{{n}_{1}}{{n}_{3}}$ | B�� | $\frac{{I}_{1}}{{I}_{2}}$=$\frac{{n}_{1}}{{n}_{2}}$��$\frac{{I}_{1}}{{I}_{3}}$=$\frac{{n}_{3}}{{n}_{1}}$ | ||
| C�� | n1I1+n3I3=n2I2 | D�� | $\frac{{I}_{1}}{{I}_{2}+{I}_{3}}$=$\frac{{n}_{2}+{n}_{3}}{{n}_{1}}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ����б������ˮƽ��н�Ϊ37�㣬�����˳����ظ����ȼ��������˶�ʱ�������е��˶����ѹ��Ϊ�����ص�$\frac{19}{16}$���������ʼ�ձ���ˮƽ����������˵�Ħ�����������صģ�sin37��=0.6��cos37��=0.8����������
��ͼ��ʾ����б������ˮƽ��н�Ϊ37�㣬�����˳����ظ����ȼ��������˶�ʱ�������е��˶����ѹ��Ϊ�����ص�$\frac{19}{16}$���������ʼ�ձ���ˮƽ����������˵�Ħ�����������صģ�sin37��=0.6��cos37��=0.8����������| A�� | $\frac{1}{4}$ | B�� | $\frac{1}{3}$ | C�� | $\frac{5}{4}$�� | D�� | $\frac{4}{3}$�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com