
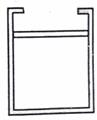
 如图所示,开口处有卡口、内横截面积为S的圆柱形气缸,缸壁导热良好,气缸内总容积为V0,大气压强为P0,一厚度不计、质量为m(m=$\frac{0.2{P}_{0}S}{g}$)的活塞封闭住一定量的理想气体,温度为T0时缸内气体体积为0.8V0,活塞与气缸内壁间无摩擦.先在活塞上缓慢放上质量为2m的砂子,然后将缸内气体温度升高到2T0.气体的内能与热力学温度的关系是U=aT,其中a为常量.求:
如图所示,开口处有卡口、内横截面积为S的圆柱形气缸,缸壁导热良好,气缸内总容积为V0,大气压强为P0,一厚度不计、质量为m(m=$\frac{0.2{P}_{0}S}{g}$)的活塞封闭住一定量的理想气体,温度为T0时缸内气体体积为0.8V0,活塞与气缸内壁间无摩擦.先在活塞上缓慢放上质量为2m的砂子,然后将缸内气体温度升高到2T0.气体的内能与热力学温度的关系是U=aT,其中a为常量.求:分析 气体先发生等温变化,然后再发生等压变化,应用玻意耳定律与盖吕萨克定律求出各状态的参量,然后根据热力学第一定律求出气体从外界吸收的热量.
解答 解:(1)活塞静止,由平衡条件得:${p}_{1}^{\;}={p}_{0}^{\;}+\frac{mg}{S}=1.2{p}_{0}^{\;}$
在活塞上缓慢放上质量为2m的砂子,由平衡条件得:
p2S=p0S+mg+2mg,
${p}_{2}^{\;}={p}_{0}^{\;}+\frac{mg}{S}=1.6{p}_{0}^{\;}$,
等温过程,由${p}_{1}^{\;}0.8{V}_{0}^{\;}={p}_{2}^{\;}{V}_{2}^{\;}$
得${V}_{2}^{\;}=0.6{V}_{0}^{\;}$,
温度升高时气体先是等压过程,直到活塞上升到卡口为止,由
$\frac{{V}_{2}^{\;}}{{T}_{0}^{\;}}=\frac{{V}_{0}^{\;}}{{T}_{1}^{\;}}$,得${T}_{1}^{\;}=\frac{5}{3}{T}_{0}^{\;}$
此后为等容过程:由得$\frac{{p}_{2}^{\;}}{{T}_{1}^{\;}}=\frac{{p}_{3}^{\;}}{{T}_{2}^{\;}}$得
${p}_{3}^{\;}=1.92{p}_{0}^{\;}$
(2)根据热力学第一定律△U=W+Q
其中$W=-{p}_{2}^{\;}({V}_{0}^{\;}-{V}_{2}^{\;})=-0.64{p}_{0}^{\;}{V}_{0}^{\;}$
$△U=a2{T}_{0}^{\;}-a{T}_{0}^{\;}=a{T}_{0}^{\;}$
所以气体温度由T0升高到2T0过程中气体吸收的热量$Q=a{T}_{0}^{\;}+0.64{p}_{0}^{\;}{V}_{0}^{\;}$
答:①温度为2T0时缸内气体的压强$1.92{p}_{0}^{\;}$.
②加完砂子后,气体温度由T0升高到2T0过程中气体吸收的热量($a{T}_{0}^{\;}+0.64{p}_{0}^{\;}{V}_{0}^{\;}$).
点评 本题是气体的状态方程与热力学第一定律结合的问题,考查综合应用物理规律的能力.关键要明确气体的物理参数变化的情况.


科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图,一个截面积为2S、盛有足够深的水的圆柱形容器放a在水平面上,容器内有一个活塞将水和一部分空气封闭,活塞能沿容器壁无摩擦滑动而不漏气.容器内水面上漂浮着一只倒扣的、薄壁圆柱形杯(杯的厚度可以忽略),其截面积为S,杯内封闭着一部分气体.当活塞与容器中杯外水面距离为H时,杯底与容器内的水面高度差为h,此时杯内气柱的高度为2h,压强与2h的水柱形成的压强相等.将活塞向下移动,使得杯底恰好与容器内的水面相平时,杯内、外水面高度均不变,杯内气柱的高度变为h,求活塞向下移动的距离x.(整个过程温度不变)
如图,一个截面积为2S、盛有足够深的水的圆柱形容器放a在水平面上,容器内有一个活塞将水和一部分空气封闭,活塞能沿容器壁无摩擦滑动而不漏气.容器内水面上漂浮着一只倒扣的、薄壁圆柱形杯(杯的厚度可以忽略),其截面积为S,杯内封闭着一部分气体.当活塞与容器中杯外水面距离为H时,杯底与容器内的水面高度差为h,此时杯内气柱的高度为2h,压强与2h的水柱形成的压强相等.将活塞向下移动,使得杯底恰好与容器内的水面相平时,杯内、外水面高度均不变,杯内气柱的高度变为h,求活塞向下移动的距离x.(整个过程温度不变)查看答案和解析>>
科目:高中物理 来源: 题型:解答题
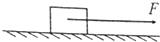 静止在水平地面上的纸箱,质量m=20kg,纸箱与地面间的动摩擦因数μ=0.2,若用水平向右,大小为50N的拉力使木箱从静止开始运动,木箱向前运动了16m(g=10m/s2)求:
静止在水平地面上的纸箱,质量m=20kg,纸箱与地面间的动摩擦因数μ=0.2,若用水平向右,大小为50N的拉力使木箱从静止开始运动,木箱向前运动了16m(g=10m/s2)求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
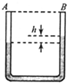 如图为一粗细均匀、足够长的等臂细U形管竖直放置,两侧上端都封闭有理想气体A、B且被水银柱隔开,已知气体A的压强PA=75.cmHg,A气柱长度为lA=20.0cm,两气柱的长度差为h=5.0cm.现将U形管水平放置,使两臂位于同一水平面上.设整个过程温度保持不变,求稳定后两空气柱的长度差h′.
如图为一粗细均匀、足够长的等臂细U形管竖直放置,两侧上端都封闭有理想气体A、B且被水银柱隔开,已知气体A的压强PA=75.cmHg,A气柱长度为lA=20.0cm,两气柱的长度差为h=5.0cm.现将U形管水平放置,使两臂位于同一水平面上.设整个过程温度保持不变,求稳定后两空气柱的长度差h′.查看答案和解析>>
科目:高中物理 来源: 题型:多选题
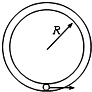 如图所示,可视为质点的、质量为m的小球,在半径为R的竖直放置的光滑圆形管道内做圆周运动,下列有关说法中正确的是( )
如图所示,可视为质点的、质量为m的小球,在半径为R的竖直放置的光滑圆形管道内做圆周运动,下列有关说法中正确的是( )| A. | 小球能够到达最高点时的最小速度为0 | |
| B. | 小球能够通过最高点时的最小速度为$\sqrt{gR}$ | |
| C. | 如果小球在最高点时的速度大小为2$\sqrt{gR}$,则此时小球对管道的内壁的作用力为3mg | |
| D. | 如果小球在最低点时的速度大小为$\sqrt{5gR}$,则小球通过最低点时对管道的外壁的作用力为6mg |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 分子间的斥力和引力随r增大而减小,在r>r0阶段,斥力比引力减小得快一些,分子间的作用力表现为引力 | |
| B. | 在r>r0阶段,F做正功,分子动能增加,势能减小 | |
| C. | 在r<r0阶段,F做负功,分子动能减小,势能也减小 | |
| D. | 在r=r0时,分子势能最小,动能最大 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,一根粗细均匀、内壁光滑、竖直放置的玻璃管下端密封,上端封闭但留有一抽气孔.管内下部被活塞封住一定质量的理想气体,气体温度为T0.开始时,活塞上方的压强为p0,长度为3L,活塞下方气柱的长度为L,活塞因重力而产生的压强为0.5p0.现将活塞上方缓慢抽成真空并密封,整个抽气过程中,管内气体温度始终保持不变.求:
如图所示,一根粗细均匀、内壁光滑、竖直放置的玻璃管下端密封,上端封闭但留有一抽气孔.管内下部被活塞封住一定质量的理想气体,气体温度为T0.开始时,活塞上方的压强为p0,长度为3L,活塞下方气柱的长度为L,活塞因重力而产生的压强为0.5p0.现将活塞上方缓慢抽成真空并密封,整个抽气过程中,管内气体温度始终保持不变.求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com