
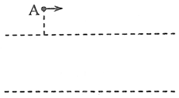
 ČēĶ¼£¬Į½ÖŹĮæĻąµČµÄŠ”Ēņ£ØŹÓĪŖÖŹµć£©M”¢NĻČŗóŅŌĻąĶ¬µÄ³õĖŁ¶ČĖ®Ę½ĻņÓŅ“ÓAµćÉä³ö£¬Į½ĒņŌŚĮ½Ė®Ę½Ćę£ØŠéĻߣ©Ö®¼äµÄĒųÓņ³żŹÜµ½ÖŲĮ¦Ķā»¹·Ö±šŹÜµ½“óŠ”ĻąµČ”¢·½ĻņĻą·“µÄĖ®Ę½ŗćĮ¦µÄ×÷ÓĆ£¬“ĖĒųÓņŅŌĶāŠ”ĒņÖ»ŹÜÖŲĮ¦×÷ÓĆ£®Į½Š”Ēņ“ÓÉĻ±ß½ē½ųČėøĆĒųÓņ£¬²¢“ÓøĆĒųÓņµÄĻĀ±ß½ēĄėæŖ£®ŅŃÖŖNĄėæŖĻĀ±ß½ēŹ±µÄĖŁ¶Č·½ĻņŹśÖ±ĻņĻĀ£»MŌŚøĆĒųÓņ×öÖ±ĻßŌĖ¶Æ£¬øÕĄėæŖøĆĒųÓņŹ±µÄ¶ÆÄÜĪŖNøÕĄėæŖøĆĒųÓņŹ±µÄ¶ÆÄܵÄ1.5±¶£®Ēó
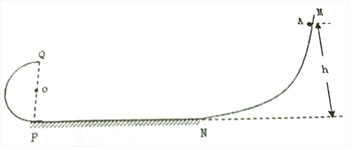
ČēĶ¼£¬Į½ÖŹĮæĻąµČµÄŠ”Ēņ£ØŹÓĪŖÖŹµć£©M”¢NĻČŗóŅŌĻąĶ¬µÄ³õĖŁ¶ČĖ®Ę½ĻņÓŅ“ÓAµćÉä³ö£¬Į½ĒņŌŚĮ½Ė®Ę½Ćę£ØŠéĻߣ©Ö®¼äµÄĒųÓņ³żŹÜµ½ÖŲĮ¦Ķā»¹·Ö±šŹÜµ½“óŠ”ĻąµČ”¢·½ĻņĻą·“µÄĖ®Ę½ŗćĮ¦µÄ×÷ÓĆ£¬“ĖĒųÓņŅŌĶāŠ”ĒņÖ»ŹÜÖŲĮ¦×÷ÓĆ£®Į½Š”Ēņ“ÓÉĻ±ß½ē½ųČėøĆĒųÓņ£¬²¢“ÓøĆĒųÓņµÄĻĀ±ß½ēĄėæŖ£®ŅŃÖŖNĄėæŖĻĀ±ß½ēŹ±µÄĖŁ¶Č·½ĻņŹśÖ±ĻņĻĀ£»MŌŚøĆĒųÓņ×öÖ±ĻßŌĖ¶Æ£¬øÕĄėæŖøĆĒųÓņŹ±µÄ¶ÆÄÜĪŖNøÕĄėæŖøĆĒųÓņŹ±µÄ¶ÆÄܵÄ1.5±¶£®Ēó·ÖĪö £Ø1£©M”¢NŌŚŹśÖ±·½ĻņĪŖ×ŌÓÉĀäĢåŌĖ¶Æ£¬øł¾Ż$h=\frac{1}{2}g{t}^{2}$æÉÖŖŹ±¼äĻąĶ¬£»
£Ø2£©×„×”Į½ĒņŌŚĒųÓņÖŠ£¬Ė®Ę½·½ĻņÉĻµÄ¼ÓĖŁ¶Č“óŠ”ĻąµČ£¬Ņ»øö×öŌČ¼ÓĖŁÖ±ĻßŌĖ¶Æ£¬Ņ»øö×öŌČ¼õĖŁÖ±ĻßŌĖ¶Æ£¬ŌŚŹśÖ±·½ĻņÉĻµÄŌĖ¶ÆŹ±¼äĻąµČµĆ³öĖ®Ę½·½ĻņŹ±¼äĻąµČ£¬½įŗĻŌĖ¶Æѧ¹«Ź½Ēó³öMÓėNŌŚĒųÓņÖŠŃŲĖ®Ę½·½ĻņµÄĪ»ŅĘÖ®±Č£»
£Ø2£©øł¾ŻĄėæŖĒųÓņŹ±¶ÆÄܵē󊔹ŲĻµ£¬×„×”M×öÖ±ĻßŌĖ¶Æ£¬µĆ³öMĄėæŖĒųÓņŹ±Ė®Ę½·ÖĖŁ¶ČŗĶŹśÖ±·ÖĖŁ¶ČµÄ¹ŲĻµ£¬×„×”MĖŁ¶Č·½Ļņ²»±ä£¬½įŗĻ½ųČėĒųÓņŹ±ŹśÖ±·ÖĖŁ¶ČŗĶĖ®Ę½·ÖĖŁ¶ČµÄ¹ŲĻµ£¬øł¾ŻĖŁ¶ČĪ»ŅĘ¹«Ź½Ēó³öAµć¾ąĒųÓņÉĻ±ß½ēµÄøß¶Č£»½įŗĻŠ”ĒņŌŚMĒųÓņÖŠ×öÖ±ĻßŌĖ¶Æ£¬½įŗĻĖŁ¶Č·½ĻņµĆ³öĖ®Ę½Į¦ŗĶÖŲĮ¦µÄ¹ŲĻµ£®
½ā“š ½ā£ŗ£Ø1£©M”¢NŌŚŹśÖ±·½ĻņĪŖ×ŌÓÉĀäĢåŌĖ¶Æ£¬øł¾Ż$h=\frac{1}{2}g{t}^{2}$æÉÖŖŹ±¼äĻąĶ¬£¬¹ŹŹ±¼äÖ®±ČĪŖ1£ŗ1£»
£Ø2£©æÉÖŖMĒņŌŚŠéĻßÖ®¼äĖ®Ę½·½ĻņÉĻ×öŌČ¼ÓĖŁÖ±ĻßŌĖ¶Æ£¬NĒņŌŚĖ®Ę½·½ĻņÉĻ×öŌČ¼õĖŁÖ±ĻßŌĖ¶Æ£¬Ė®Ę½·½ĻņÉĻµÄ¼ÓĖŁ¶Č“óŠ”ĻąµČ£¬
Į½ĒņŌŚŹśÖ±·½Ļņ¾łŹÜÖŲĮ¦£¬ŹśÖ±·½ĻņÉĻ×ö¼ÓĖŁ¶ČĪŖgµÄŌČ¼ÓĖŁÖ±ĻßŌĖ¶Æ£¬ÓÉÓŚŹśÖ±·½ĻņÉĻµÄĪ»ŅĘĻąµČ£¬ŌņŌĖ¶ÆµÄŹ±¼äĻąµČ£¬
ÉčĖ®Ę½·½ĻņµÄ¼ÓĖŁ¶Č“óŠ”ĪŖa£¬
¶ŌM£¬ÓŠ£ŗxM=v0t+$\frac{1}{2}$at2
¶ŌN£ŗv0=at£¬xN=$\frac{1}{2}$at2
æÉµĆ£ŗxM=$\frac{3}{2}$at2
½āµĆ£ŗxM£ŗxN=3£ŗ1
£Ø3£©ÉčMŠ”ĒņĄėæŖĒųÓņŹ±µÄŹśÖ±·ÖĖŁ¶ČĪŖvy£¬Ė®Ę½·ÖĖŁ¶ČĪŖv1£¬Į½ĒņĒųÓņŹ±ŹśÖ±·ÖĖŁ¶ČĻąµČ£¬
ŅņĪŖMŌŚĒųÓņÖŠ×öÖ±ĻßŌĖ¶Æ£¬øÕĄėæŖĒųÓņŹ±µÄ¶ÆÄÜĪŖNøÕĄėæŖĒųÓņŹ±µÄ¶ÆÄܵÄ1.5±¶£¬ŌņÓŠ£ŗ
$\frac{1}{2}m£Ø{v}_{y}^{2}+{v}_{1}^{2}£©$=$1.5•\frac{1}{2}m{v}_{y}^{2}$
½āµĆ£ŗ${v}_{1}=\frac{\sqrt{2}}{2}{v}_{y}$
ŅņĪŖv1=v0+at=2v0£¬Ōņv1=2v0
ŅņĪŖM×öÖ±ĻßŌĖ¶Æ£¬É芔Ēņ½ųĒųÓņŹ±ŌŚŹśÖ±·½ĻņÉĻµÄ·ÖĖŁ¶ČĪŖvy1£¬ŌņÓŠ£ŗ
$\frac{{v}_{y1}}{{v}_{0}}$=$\frac{{v}_{y}}{{v}_{1}}$
½āµĆ£ŗvy1=$\frac{1}{2}{v}_{y}$
ŌŚŹśÖ±·½ĻņÉĻÓŠ£ŗ${v}_{y1}^{2}=2gh$£¬${v}_{y}^{2}-{v}_{y1}^{2}=2gH$
½āµĆAµć¾ąĒųÓņÉĻ±ß½ēµÄø߶Čh=$\frac{1}{3}H$
ŅņĪŖM×öÖ±ĻßŌĖ¶Æ£¬ŗĻĮ¦·½ĻņÓėĖŁ¶Č·½ĻņŌŚĶ¬Ņ»ĢõÖ±ĻßÉĻ£¬
ÓŠ£ŗ$\frac{{v}_{y}}{{v}_{1}}=\frac{mg}{F}=\sqrt{2}$$\frac{{v}_{1}}{{v}_{y}}=\frac{F}{mg}=\frac{\sqrt{2}}{2}$
“š£ŗ£Ø1£©M“ÓAµćÉä³öæŖŹ¼µ½øÕĄėæŖĻĀ±ß½ēĖłÓĆŹ±¼äÓėN“ÓAµćÉä³öæŖŹ¼µ½øÕĄėæŖĻĀ±ß½ēĖłÓĆŹ±¼äµÄ±ČĪŖ1£ŗ1£»
£Ø2£©MÓėNŌŚĮ½Ė®Ę½Ćę£ØŠéĻߣ©Ö®¼äµÄĒųÓņŃŲĖ®Ę½·½ĻņµÄĪ»ŅĘÖ®±ČĪŖ3£ŗ1£»
£Ø3£©MŌŚĮ½Ė®Ę½Ćę£ØŠéĻߣ©Ö®¼äµÄĒųÓņĖłŹÜµ½µÄĖ®Ę½Į¦“óŠ”ÓėÖŲĮ¦“óŠ”Ö®±ČĪŖ$\sqrt{2}£ŗ2$£®
µćĘĄ ±¾ĢāÖŲŌŚĄķĒåĮ½ĒņŌŚÕūøö¹ż³ĢÖŠµÄŌĖ¶Æ¹ęĀÉ£¬½«ŌĖ¶Æ·Ö½āĪŖĖ®Ę½·½ĻņŗĶŹśÖ±·½Ļņ£¬½įŗĻŌĖ¶Æѧ¹«Ź½Įé»īĒó½ā£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗøßÖŠĪļĄķ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
 ČēĶ¼ĖłŹ¾£¬ÓĆµÆ»É³ÓŹśÖ±ĻņÉĻĄĖ®Ę½µŲĆęÉĻµÄĪļæ飬ĪļæéŹÜµ½µÄÖŲĮ¦ĪŖ15N£®ČōµÆ»É³ÓµÄŹ¾ŹżĪŖ8N£¬ŌņµŲĆę¶ŌĪļæéµÄµÆĮ¦ŹĒ£Ø””””£©
ČēĶ¼ĖłŹ¾£¬ÓĆµÆ»É³ÓŹśÖ±ĻņÉĻĄĖ®Ę½µŲĆęÉĻµÄĪļæ飬ĪļæéŹÜµ½µÄÖŲĮ¦ĪŖ15N£®ČōµÆ»É³ÓµÄŹ¾ŹżĪŖ8N£¬ŌņµŲĆę¶ŌĪļæéµÄµÆĮ¦ŹĒ£Ø””””£©| A£® | 7N£¬·½ĻņŹśÖ±ĻņÉĻ | B£® | 8N£¬·½ĻņŹśÖ±ĻņĻĀ | ||
| C£® | 15N£¬·½ĻņŹśÖ±ĻņÉĻ | D£® | 15N£¬·½ĻņŹśÖ±ĻņĻĀ |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠĪļĄķ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠĪļĄķ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | v£¬2v | B£® | 0£¬2v | C£® | 0£¬v | D£® | 0.5v£¬1.5v |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠĪļĄķ Ą“Ō“£ŗ ĢāŠĶ£ŗ¶ąŃ”Ģā
| A£® | ĆæøöŠ”ĒņŌŚæÕÖŠŌĖ¶ÆµÄ¹ģ¼£ĪŖÅ×ĪļĻß | |
| B£® | ĻąĮŚĮ½Š”Ēņ¼äĖ®Ę½·½ĻņÉĻµÄ¾ąĄėÖ®±ČĪŖ1£ŗ2£ŗ3 | |
| C£® | ŌŚDĒņæŖŹ¼ĻĀĀäµÄĖ²Ź±£¬ĻąĮŚĮ½ĒņµÄ¼ä¾ą$\overline{AB}$”¢$\overline{BC}$”¢$\overline{CD}$Ö®±ČĪŖ5£ŗ3£ŗ1 | |
| D£® | ŌŚĻąĶ¬µÄŹ±¼äÄŚ£¬ĖÄøöŠ”ĒņµÄĖŁ¶ČøıäĮæ“óŠ”ĻąµČ”¢·½ĻņĻąĶ¬ |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠĪļĄķ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | µ„°Ś×ö¼ņŠ³ŌĖ¶ÆµÄ»Ųø“Į¦ŹĒÖŲĮ¦ŗĶ°ŚĻߥĮ¦µÄŗĻĮ¦ | |
| B£® | °ŚĒņ×÷¼ņŠ³Õń¶ÆĪ»ŅĘ×ī“󓦏±£¬¼ÓĖŁ¶Č×ī“󣬰ŚĻߥĮ¦ĪŖĮć | |
| C£® | °ŚĒņ¾Ę½ŗāĪ»ÖĆŹ±£¬°ŚĻߥĮ¦×ī“󣬻Ųø“Į¦ĪŖĮć | |
| D£® | µ„°ŚµÄÕń¶ÆŅ»¶ØŹĒ¼ņŠ³Õń¶Æ |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠĪļĄķ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | 20m | B£® | 9m | C£® | 12m | D£® | 16m |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠĪļĄķ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
 ÖŹµć×öÖ±ĻßŌĖ¶ÆµÄv-tĶ¼ĻóČēĶ¼ĖłŹ¾£¬¹ę¶ØĻņÓŅĪŖÕż·½Ļņ£¬ŌņøĆÖŹµćŌŚĒ°8sÄŚĘ½¾łĖŁ¶ČµÄ“óŠ”ŗĶ·½Ļņ·Ö±šĪŖ£Ø””””£©
ÖŹµć×öÖ±ĻßŌĖ¶ÆµÄv-tĶ¼ĻóČēĶ¼ĖłŹ¾£¬¹ę¶ØĻņÓŅĪŖÕż·½Ļņ£¬ŌņøĆÖŹµćŌŚĒ°8sÄŚĘ½¾łĖŁ¶ČµÄ“óŠ”ŗĶ·½Ļņ·Ö±šĪŖ£Ø””””£©| A£® | 0.25 m/s””ĻņÓŅ | B£® | 0.25 m/s””Ļņ×ó | C£® | 1 m/s””ĻņÓŅ | D£® | 1 m/sĻņ×ó |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠĪļĄķ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
 ČēĶ¼ĖłŹ¾£¬Ņ»øö²»“ųµēµÄ½šŹōĒņ·ÅŌŚŅ»øöµēĮæĪŖ+QµÄµćµēŗÉø½½ü£¬½šŹōĒņµÄ°ė¾¶ĪŖr£¬µćµēŗɵ½½šŹōĒņĒņŠÄOµÄ¾ąĄėĪŖR£¬Ōņ½šŹōĒņÉĻøŠÓ¦µēŗÉŌŚOµć²śÉśµÄ³”Ēæ“óŠ”ĪŖ$\frac{kQ}{{R}^{2}}$£¬·½ĻņĖ®Ę½ĻņÓŅ£®
ČēĶ¼ĖłŹ¾£¬Ņ»øö²»“ųµēµÄ½šŹōĒņ·ÅŌŚŅ»øöµēĮæĪŖ+QµÄµćµēŗÉø½½ü£¬½šŹōĒņµÄ°ė¾¶ĪŖr£¬µćµēŗɵ½½šŹōĒņĒņŠÄOµÄ¾ąĄėĪŖR£¬Ōņ½šŹōĒņÉĻøŠÓ¦µēŗÉŌŚOµć²śÉśµÄ³”Ēæ“óŠ”ĪŖ$\frac{kQ}{{R}^{2}}$£¬·½ĻņĖ®Ę½ĻņÓŅ£®²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com