Question

（25分）如图预19-7所示，在长为m、质量为的车厢B内的右壁处，放一质量的小物块A（可视为质点），向右的水平拉力作用于车厢，使之从静止开始运动，测得车厢B在最初2.0 s内移动的距离，且在这段时间内小物块未与车厢壁发生过碰撞．假定车厢与地面间的摩擦忽略不计，小物块与车厢壁之间的碰撞是弹性的．求车厢开始运动后4.0 s时，车厢与小物块的速度．

Answer 1

参考解答

解法一：

1. 讨论自B开始运动到时间内B与A的运动。

根据题意，在2 s内，A未与B发生过碰撞，因此不论A与B之间是否有相对运动，不论A与B之间是否有摩擦，B总是作初速为零的匀加速直线运动。设B的加速度为，有

           

得

                                     （1）

如果A、B之间无摩擦，则在B向右移动1米距离的过程中，A应保持静止状态，接着B的车厢左壁必与A发生碰撞，这不合题意。如果A、B之间无相对运动（即两者之间的摩擦力足以使A与B有一样的加速度），则B的加速度

这与（1）式矛盾。由此可见，A、B之间既有相对运动又存在摩擦力作用。

以表示A、B间的滑动摩擦力的大小，作用于B的摩擦力向左，作用于A的摩擦力向右，则有

                                                     （2）

                                              （3）

由（1）、（2）、（3）式得

                                         （4）

                                               （5）

2. 讨论B的左壁与A发生第一次碰撞前的运动。

由于，B向右的速度将大于A的速度，故A与B的左壁间的距离将减小。设自静止开始，经过时间，B的左壁刚要与A发生碰撞，这时，B向右运动的路程与A向右运动的路程之差正好等于，即有

            

解得

                                                          （6）

代入数据，得

                

A与B发生第一次碰撞时，碰前的速度分别为

                                                （7）

                                                （8）

3. 讨论B与A间的弹性碰撞

以和分别表示第一次碰撞后A和B的速度。当、为正时，分别表示它们向右运动。在碰撞的极短时间内，外力的冲量可忽略不计，因此有

            

                

解以上两式得

                                     （9）

（9）式表示，在弹性碰撞中，碰撞前后两者的相对速度的大小不变，但方向反转。

4. 讨论从第一次碰撞到车厢与小物块速度变至相同过程中的运动。

由（9）式可以看出，经第一次碰撞，A和B都向右运动，但A的速度大于B的速度，这时作用于A的摩擦力向左，作用于B的摩擦力向右，大小仍都为。设此过程中A向左的加速度和B向右的加速度分别为和，则由牛顿第二定律有

            

            

解得

                                                   （10）

                                                 （11）

由此可知，碰撞后，A作减速运动，B作加速运动。设经过时间，两者速度相等，第一次达到相对静止，则有

                

由上式和（9）式解得

                                  （12）

代入有关数据得

                                                        （13）

设在时间内，A与B的左壁之间的距离增大至，则有

                

结合（9）、（12）两式得

                                                                            （14）

式中

                                                          （15）

代入有关数据得

                

由（14）可知，A不会与B的右壁发生碰撞。

5. 讨论A与B的左壁的第二次碰撞。

以表示B与A第一次相等的速度，由于B始终受作用而加速，它将拖着A向右加速，其情况与第一次碰撞前相似。这时作用于A的摩擦力向右，A的加速度为，方向向右。作用于B的摩擦力向左，B的加速度为，方向也向右。但是原来A与B左端的距离为，现改为，因，B的左壁与小A之间的距离将减小。设两者间的距离从减小至零即减小至开始发生第二次碰撞所经历的时间为，以代入⑥式，结合（14）式，即可求得

                                    （16）

代入有关数据，得

                

第二次碰撞前瞬间A和B的速度分别为

                

                

                         （17）

故第二次碰撞前A、B速度之差小于第一次碰撞前A、B的速度差。设第二次碰撞完毕的瞬间A、B的速度分别为和，则有

                                      （18）

第二次碰撞后，A以加速度作减速运动，B以加速度作加速运动。设经历时间，两者速度相等，即第二次相对静止，则有

                

解得

                                  （19）

在时间内，A与B的左壁的距离变为，有

                

结合（8）、（9）得

                                                                  （20）

自B开始运动到A与B达到第二次相对静止共经历时间

                

                

6. 讨论A与B的左壁的第三次碰撞。

当A与B的左壁之间的距离为时，A、B相对静止。由于B受外力作用而继续加速，它将拖着A向右加速。这时，A的加速度为，B的加速度为，方向都向右，但因，A将与B的左壁发生第三次碰撞。设此过程经历的时间为，则以代入（6）式结合（16）式得

                         （21）

设第三次碰撞前瞬间A和B的速度分别为和，碰撞后的速度分别为和

                

碰撞后，A以加速度作减速运动，B以加速度作加速运动。设经过时间两者速度相等，即第三次相对静止，A与B左壁之间的距离为。则有

                                                    （22）

                   

自B开始运动至第三次A与B相对静止共经历的时间仍小于4 s。

7. 讨论车厢左壁与小物块的第次碰撞。

在第次碰撞完毕的瞬间，A和B的速度分别为和，A以加速度作减速运动，B以加速度作加速运动。经过时间，两者速度相等，即第次相对静止。A与B左壁之间的距离为。根据前面的讨论有

                                                            （23）

                

再经过时间将发生B的左壁与A的第次碰撞。碰撞前两者的速度分别为和。根据前面的讨论，有

                                                             （24）

                

可以看出，碰撞次数越多，下一次碰撞前，A、B速度之差越小。当碰撞次数非常大时，下次碰撞前两者的速度趋于相等，即A实际上将贴在B的左壁上不再分开。

8. 讨论第4秒B与A的运动速度。

第4秒末B与A的速度取决于在第4秒末B与A经历了多少次碰撞。B自静止开始运动到第次相对静止经历的总时间为

             

                                           （25）

以，代入，注意到当很大时，得

                                                    （26）

这表明早在第4秒之前，A与B的左壁贴在一起时二者速度已相同，不再发生碰撞，此后二者即以相同的速度运动了、现以A和B都静止时作为初态，设时刻A和B的速度为，对A、B开始运动至的过程应用动量定理，得

                                                       （27）

或

                

代入数值，得

                                                          （28）

解法二：

如果A与B之间没有摩擦力，B前进1m就会与A发生碰撞。已知开始2s为A与B未发生碰撞，而B已走了5m，可见二者之间有摩擦力存在，且在此期间二者均作匀加速运动。由可求出B对地面的加速度：

            ，                              

设A与B底部之间的滑动摩擦力为，则由小车的运动方程

                

代入数值得

                                                                

又由A的运动方程得A的相对地面的加速度为

                                                    

于是，A对B的相对加速度为

                                             

第一次碰撞

由开始运动到A碰撞B的左壁的时间满足，。于是

                                                     

A与B的左壁碰撞前瞬间，A相对B的速度

                                  

由于作弹性碰撞的两个物体在碰撞前后其相对速度等值反向，所以碰后A从B的左壁开始，以相对速度

                                    

向右运动，所受摩擦力反向向左，为。对地面的加速度为

                                                  

此时B所受的摩擦力方向向右，由其运动方程得B对地面的加速度为

                                                  

由、二式知，碰后A对B的相对加速度为

                                             

A相当于B作向右的匀减速运动。设A由碰后开始达到相对静止的时间为，相当于B走过的距离为，由式得

                                        

                              

可见A停止在B当中，不与B的右壁相碰。

第二次碰撞

A在B内相对静止后，将相当于B向左滑动，所受的摩擦力改为向右，而B所受的摩擦力改为向左。这时A对B的相对加速度重新成为，即式。A由相对静止到与B的左壁第二次碰撞所需的时间可用算出：

                                

自B开始运动至B的左壁与A发生第二次碰撞经历的时间

                

A达到B的左壁前相当于B的速度的大小为

                                   

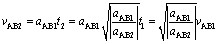
这也就是第二次碰后A由B的左壁出发的相对速度大小。第二次碰后，A相对B向右运动，此时A相对于B的相对加速度又成为，即式。A由碰撞到相对静止所需要的时间和相当于B走过的距离分别为

                     

                

以后的碰撞

根据、二式，如令

                                      

则有

                   

由此可以推知，在第三次碰撞中必有

                                                

在第次碰撞中有

                                                      

即每一次所需时间要比上次少得多（A在B中所走的距离也小得多）。把所有的时间加在一起，得

          

这就是说，在B开始运动后3.56 s时，A将紧贴B的左壁，并与B具有相同速度，二者不再发生碰撞，一直处于相对静止状态。现取A和B都静止时作为初态，以时刻的运动状态为末态，设此时A和B的速度为，由动量定理，有

                

代入数值，得

                                                 

答：自车厢开始运动到4.0 s时车厢与物块的速度相同，均为

评分标准：本题25分。

得出摩擦力得5分，得出第一次碰撞时间得5分，得出第二次碰撞时间得5分。得出无穷次碰撞时间得5分 ，得到最后结果再得5分。