
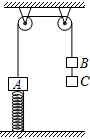
 如图所示,一轻质弹簧下端固定在水平地面上,上端与物体A连接,物体A又与一跨过定滑轮的不可伸长的轻绳一端相连,绳另一端悬挂着物体B,B的下面又挂着物体C,A、B、C均处于静止状态.现剪断B和C之间的绳子,则A和B将做简谐运动.已知物体A质量为3m,B和C质量均为2m,A和B振动的振幅为d.试求:
如图所示,一轻质弹簧下端固定在水平地面上,上端与物体A连接,物体A又与一跨过定滑轮的不可伸长的轻绳一端相连,绳另一端悬挂着物体B,B的下面又挂着物体C,A、B、C均处于静止状态.现剪断B和C之间的绳子,则A和B将做简谐运动.已知物体A质量为3m,B和C质量均为2m,A和B振动的振幅为d.试求: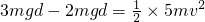 ,解得v=
,解得v=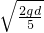 .
.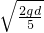 .
.

科目:高中物理 来源: 题型:
 如图所示,一轻质弹簧竖直放置,下端固定在水平面上,上端处于a位置.当一重球放在弹簧上端静止时,弹簧上端被压缩到b位置.现将重球(视为质点)轻放在弹簧a处,由静止释放后,球沿弹簧中轴线向下运动到最低点c处的过程中,下列说法正确的是( )
如图所示,一轻质弹簧竖直放置,下端固定在水平面上,上端处于a位置.当一重球放在弹簧上端静止时,弹簧上端被压缩到b位置.现将重球(视为质点)轻放在弹簧a处,由静止释放后,球沿弹簧中轴线向下运动到最低点c处的过程中,下列说法正确的是( )查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,一轻质弹簧与质量为m的物体组成弹簧振子,物体在同一条竖直线上的A、B间做简谐运动,O为平衡位置,C为AO的中点,已知OC=h,振子的周期为T.某时刻物体恰好经过C点并向上运动,则从此时刻开始的半个周期时间内,下列判断正确的是( )
如图所示,一轻质弹簧与质量为m的物体组成弹簧振子,物体在同一条竖直线上的A、B间做简谐运动,O为平衡位置,C为AO的中点,已知OC=h,振子的周期为T.某时刻物体恰好经过C点并向上运动,则从此时刻开始的半个周期时间内,下列判断正确的是( )查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,一轻质弹簧固定在水平地面上,O点为弹簧原长时上端的位置,一个质量为m的物体从O点正上方的A点由静止释放落到弹簧上,物体压缩弹簧到最低点B 后向上运动.则以下说法正确的是( )
如图所示,一轻质弹簧固定在水平地面上,O点为弹簧原长时上端的位置,一个质量为m的物体从O点正上方的A点由静止释放落到弹簧上,物体压缩弹簧到最低点B 后向上运动.则以下说法正确的是( )查看答案和解析>>
科目:高中物理 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com