
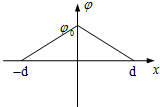
 静电场方向平行于x轴,其电势φ随x的分布可以简化为如图所示的折线,图中φ0和d为已知量.一个重力不计,质量为m,带电量为-q的负电粒子在电场中,以x=0为中心,沿x轴方向在[-A,A]间做周期运动(A<d).求:
静电场方向平行于x轴,其电势φ随x的分布可以简化为如图所示的折线,图中φ0和d为已知量.一个重力不计,质量为m,带电量为-q的负电粒子在电场中,以x=0为中心,沿x轴方向在[-A,A]间做周期运动(A<d).求:分析 (1)由图可知,电势随x均匀变化,则可知电场为匀强电场,由电势差与电场强度的关系可求得电场强度,即可求得电场力;
(2)由题意可知,动能与电势能之和保持不变,设出运动区间为[-x,x],由题意可知x处的电势,则由数学关系可求得x值
(3)粒子在区间内做周期性变化,且从最远点到O点时做匀变速直线运动,则由运动学规律可求得周期
解答 解:(1)-d≤x≤0区间 $k=\frac{ϕ_0}{d}$
故:$ϕ=\frac{ϕ_0}{d}x+{ϕ_0}={ϕ_0}(\frac{x}{d}+1)$(-d≤x≤0
0≤x≤d区间 $k=-\frac{ϕ_0}{d}$
故:$ϕ=-\frac{ϕ_0}{d}x+{ϕ_0}={ϕ_0}(1-\frac{x}{d})$(0≤x≤d)
或在整个区域内,$ϕ={ϕ_0}(1-\frac{1x1}{d})$(x<d)
由图可知电场强度大小$E=\frac{ϕ_0}{d}$
则电场力大小$F=qE=\frac{{q{ϕ_0}}}{d}$
(2)0≤x≤A区间
根据题意,在x=A时,粒子动能为0,
可知粒子在运动过程中动能和电势能之和为:
则在x位置时有:${E_k}+(-qϕ)=-q{ϕ_0}(1-\frac{A}{d})$
${E_k}-q{ϕ_0}(1-\frac{x}{d})=-q{ϕ_0}(1-\frac{A}{d})$${E_k}=q{ϕ_0}\frac{(A-x)}{d}$(0≤x≤A)
-A≤x≤0区间
根据题意,在x=-A时,粒子动能为0,可知粒子在运动过程中动能和电势能之和为:
则在x位置时有:${E_k}+(-qϕ)=-q{ϕ_0}(1-\frac{A}{d})$
${E_k}-q{ϕ_0}(\frac{x}{d}+1)=-q{ϕ_0}(1-\frac{A}{d})$${E_k}=q{ϕ_0}\frac{(A+x)}{d}$(-A≤x≤0)
或者:${E_k}=q{ϕ_0}\frac{(A-1x1)}{d}$(-A≤x≤A)
(3)0-A为四分之一周期,粒子做匀变速直线运动
S=A,$a=\frac{F}{m}=\frac{{q{ϕ_0}}}{dm}$
$t=\sqrt{\frac{2s}{a}}=\sqrt{\frac{2mdA}{{q{ϕ_0}}}}$
$T=4t=4\sqrt{\frac{2mdA}{{q{ϕ_0}}}}$
答:(1)写出电势随x的变化规律关系式为$ϕ={ϕ}_{0}(1-\frac{1x1}{d})$,粒子所受电场力大小为$\frac{q{ϕ}_{0}}{d}$
(2)粒子动能随x的变化规律关系式${E}_{k}=q{ϕ}_{0}\frac{(A-1x1)}{d}$
(3)粒子的运动周期$T=4\sqrt{\frac{2mdA}{q{ϕ}_{0}}}$.
点评 本题难度较大,要求学生能从题干中找出可用的信息,同时能从图象中判断出电场的性质;并能灵活应用功能关系结合数学知识求解,故对学生的要求较高


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中物理 来源: 题型:选择题
| A. | g-a,v | B. | g+a,v | C. | a,0 | D. | g,v |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 太阳的质量为$\frac{{4{π^2}R_1^2}}{GT_2^2}$ | |
| B. | 天王星公转速度大于地球公转速度 | |
| C. | 地球与天王相距最近至少需经历$\frac{{{T_1}{T_2}}}{{2({{T_1}-{T_2}})}}$ | |
| D. | 天王星公转的向心加速度与地球公转的向心加速度之比为$\frac{R_1^2}{R_2^2}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 温度升高时物体内的每个分子的运动速率一定增大 | |
| B. | 同种物质可能以晶体和非晶体两种不同的形态出现 | |
| C. | 物体吸热内能一定增大 | |
| D. | 不断改进工艺,热机的效率可能达到100% |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
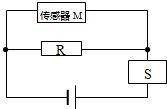 在输液时,药液有时会从针口流出体外,为了及时发现,设计了一种报警装置.电路如图所示,M是贴在针口处的传感器,接触到药液时其电阻RM会发生变化,导致S两端的电压U增大而报警.此时( )
在输液时,药液有时会从针口流出体外,为了及时发现,设计了一种报警装置.电路如图所示,M是贴在针口处的传感器,接触到药液时其电阻RM会发生变化,导致S两端的电压U增大而报警.此时( )| A. | RM变大,且R越大,U增大越明显 | B. | RM变大,且R越小,U增大越明显 | ||
| C. | RM变小,且R越大,U增大越明显 | D. | RM变小,且R越小,U增大越明显 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 匀速圆周运动 | B. | 匀加速直线运动 | C. | 类平抛运动 | D. | 匀减速直线运动 |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
 一质量为2kg的质点在0~15s内由静止开始从地面竖直向上运动,取竖直向上为正方向,得到如图所示的加速度和时间的变化关系图象.当t3=15s时,质点的速度大小为40m/s;若以地面为零势能面,则t1=5s与t3=15s两个时刻质点的机械能之比为25:28.
一质量为2kg的质点在0~15s内由静止开始从地面竖直向上运动,取竖直向上为正方向,得到如图所示的加速度和时间的变化关系图象.当t3=15s时,质点的速度大小为40m/s;若以地面为零势能面,则t1=5s与t3=15s两个时刻质点的机械能之比为25:28.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 物体A的质量为mA,圆环B的质量为mB,通过绳子连结在一起,圆环套在光滑的竖直杆上,开始时连接圆环的绳子处于水平,如图所示,长度l=4m,现从静止释放圆环.不计定滑轮和空气的阻力,取g=10m/s2.求:
物体A的质量为mA,圆环B的质量为mB,通过绳子连结在一起,圆环套在光滑的竖直杆上,开始时连接圆环的绳子处于水平,如图所示,长度l=4m,现从静止释放圆环.不计定滑轮和空气的阻力,取g=10m/s2.求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,物体从斜面ab上高为h的M点由静止起下滑,经过水平地面bc后再沿光滑斜面cd恰能上滑到高为$\frac{h}{2}$的N点,现将物体以初速度v0仍自M点沿斜面下滑后经bc再沿cd恰能上滑到高为h处,则v0的大小为( )
如图所示,物体从斜面ab上高为h的M点由静止起下滑,经过水平地面bc后再沿光滑斜面cd恰能上滑到高为$\frac{h}{2}$的N点,现将物体以初速度v0仍自M点沿斜面下滑后经bc再沿cd恰能上滑到高为h处,则v0的大小为( )| A. | $\sqrt{gh}$ | B. | $\sqrt{2gh}$ | C. | $\sqrt{3gh}$ | D. | 2$\sqrt{gh}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com