
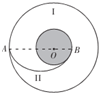
 开普勒第三定律指出:所有行星的轨道的半长轴的三次方跟它的公转周期的二次方的比值都相等.该定律对一切具有中心天体的引力系统都成立.如图,嫦娥三号探月卫星在半径为r的圆形轨道I上绕月球运行,周期为T.月球的半径为R,引力常量为G.某时刻嫦娥三号卫星在4点变轨进入椭圆轨道II,在月球表面的B点着陆.A、O、B三点在一条直线上.
开普勒第三定律指出:所有行星的轨道的半长轴的三次方跟它的公转周期的二次方的比值都相等.该定律对一切具有中心天体的引力系统都成立.如图,嫦娥三号探月卫星在半径为r的圆形轨道I上绕月球运行,周期为T.月球的半径为R,引力常量为G.某时刻嫦娥三号卫星在4点变轨进入椭圆轨道II,在月球表面的B点着陆.A、O、B三点在一条直线上.分析 (1)根据万有引力提供向心力,结合卫星的轨道半径和周期求出月球的质量,根据月球的体积求出月球的密度.
(2)根据几何关系求出椭圆轨道的半长轴,结合开普勒第三定律求出在II轨道上运行的时间.
解答 解:(1)由万有引力充当向心力:$\frac{GMm}{r^2}=m{(\frac{2π}{T})^2}r$,
解得$M=\frac{{4{π^2}{r^3}}}{{G{T^2}}}$
月球的密度:$ρ=\frac{M}{{\frac{4}{3}π{R^3}}}$,解得$ρ=\frac{{3π{r^3}}}{{G{T^2}{R^3}}}$.
(2)椭圆轨道的半长轴:$a=\frac{R+r}{2}$,
设椭圆轨道上运行周期为T1,由开普勒第三定律有:$\frac{a^3}{T_1^2}=\frac{r^3}{T^2}$,
在Ⅱ轨道上运行的时间为t:$t=\frac{T_1}{2}$,
解得$t=\frac{(R+r)T}{4r}\sqrt{\frac{(R+r)}{2r}}$.
答:(1)月球的密度为$\frac{3π{r}^{3}}{G{T}^{2}{R}^{3}}$;
(2)在II轨道上运行的时间为$\frac{(R+r)T}{4r}\sqrt{\frac{(R+r)}{2r}}$.
点评 本题考查了万有引力定律和开普勒第三定律的综合运用,知道在Ⅱ轨道上运行的时间等于椭圆轨道运动周期的一半,结合开普勒第三定律进行求解.


科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
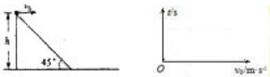
 如图所示,在水平面上受到斜向下推力F作用的物体,处于静止状态.关于物体受力,下列说法中正确的是( )
如图所示,在水平面上受到斜向下推力F作用的物体,处于静止状态.关于物体受力,下列说法中正确的是( )| A. | 静摩擦力大于F | B. | 静摩擦力小于F | ||
| C. | 支持力小于重力 | D. | 支持力与重力的大小相等 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
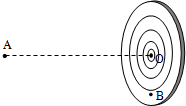 如图所示,一个半径R=$\frac{5}{16}$m的圆形靶盘竖直放置,A、O两点等高且相距4m,将质量为20g的飞镖从A点沿AO方向抛出,经0.2s落在靶心正下方的B点处.不计空气阻力,重力加速度取g=10m/s2.求:
如图所示,一个半径R=$\frac{5}{16}$m的圆形靶盘竖直放置,A、O两点等高且相距4m,将质量为20g的飞镖从A点沿AO方向抛出,经0.2s落在靶心正下方的B点处.不计空气阻力,重力加速度取g=10m/s2.求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 某同学通过下述实验验证力的平行四边形定则.实验步骤:
某同学通过下述实验验证力的平行四边形定则.实验步骤:| F(N) | 0 | 0.50 | 1.00 | 1.05 | 2.00 | 2.50 |
| l (cm) | l0 | 10.97 | 12.02 | 13.00 | 13.98 | 15.05 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 某物理实验小组在探究弹簧的劲度系数k与其原长l0的关系实验中,按示意图所示安装好实验装置,让刻度尺零刻度与轻质弹簧上端平齐,在弹簧上安装可移动的轻质指针P,实验时的主要步骤是:
某物理实验小组在探究弹簧的劲度系数k与其原长l0的关系实验中,按示意图所示安装好实验装置,让刻度尺零刻度与轻质弹簧上端平齐,在弹簧上安装可移动的轻质指针P,实验时的主要步骤是:| 次数 | 弹簧原长l0/cm | 弹簧长度l/cm | 钩码质量m/g |
| 1 | 5.00 | 7.23 | 200 |
| 2 | 10.00 | 15.56 | 250 |
| 3 | 15.00 | 16.67 | 50 |
| 4 | 20.00 | 22.23 | 50 |
| 5 | 25.00 | 30.56 | 50 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
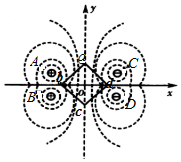 如图所示,在平面直角坐标系xOy内,固定有A、B、C、D四个带电量均为Q的点电荷,它们关于两坐标轴对称,其中A、B带正电,C、D带负电,它们产生电场的等势面如图中虚线所示,坐标轴上abcd是图中正方形的四个顶点,则( )
如图所示,在平面直角坐标系xOy内,固定有A、B、C、D四个带电量均为Q的点电荷,它们关于两坐标轴对称,其中A、B带正电,C、D带负电,它们产生电场的等势面如图中虚线所示,坐标轴上abcd是图中正方形的四个顶点,则( )| A. | b、d两点电势相等,场强不相等 | |
| B. | b、d两点场强相同,电势不相等 | |
| C. | 将电子沿路径a→O→c移动,电场力做正功 | |
| D. | 将电子沿路径a→b→c移动,电场力先做负功,后做正功 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
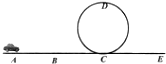 低碳环保绿色出行的理念逐渐深入人心,而纯电动汽车是时下相对较环保的汽车,为宣传“低碳环保”健康生活理念,某次志愿者举行玩具电动小汽车的表演,如图所示,质量m=2kg的小汽车以vo=4m/s的初速度从水平轨迹A处出发,沿平直轨道AC运动,到达C点时关闭发动机,进入半径R=1.8m圆轨道,恰能做完整的圆周运动后又进入CE水平轨道向右运动,直至停下,已知小汽车与水平面的摩擦阻力恒为重力的0.1倍,AB段运动过程中风力较大,可能化为受0.8N的水平向左的作用力,过B点后小汽车所受空气作用力均忽略不计,圆轨道可视作光滑,已知AB段长度x1=3m,BC段长度x2=2m,CE段足够长,小汽车自身长度可忽略,求:
低碳环保绿色出行的理念逐渐深入人心,而纯电动汽车是时下相对较环保的汽车,为宣传“低碳环保”健康生活理念,某次志愿者举行玩具电动小汽车的表演,如图所示,质量m=2kg的小汽车以vo=4m/s的初速度从水平轨迹A处出发,沿平直轨道AC运动,到达C点时关闭发动机,进入半径R=1.8m圆轨道,恰能做完整的圆周运动后又进入CE水平轨道向右运动,直至停下,已知小汽车与水平面的摩擦阻力恒为重力的0.1倍,AB段运动过程中风力较大,可能化为受0.8N的水平向左的作用力,过B点后小汽车所受空气作用力均忽略不计,圆轨道可视作光滑,已知AB段长度x1=3m,BC段长度x2=2m,CE段足够长,小汽车自身长度可忽略,求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com