
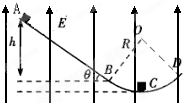
 如图所示,AB是一倾角为θ=37°的绝缘粗糙直轨道,滑块与斜面间的动摩擦因数μ=0.30,BCD是半径为R=0.2m的光滑圆弧轨道,它们相切于B点,C为圆弧轨道的最低点,整个空间存在着竖直向上的匀强电场,场强E=4.0×103N/C,质量m=0.20kg的带电滑块从斜面顶端由静止开始滑下.已知斜面AB对应的高度h=0.24m,滑块带电荷q=-5.0×10-4C,取重力加速度g=10m/s2,sin37°=0.60,cos37°=0.80.求:
如图所示,AB是一倾角为θ=37°的绝缘粗糙直轨道,滑块与斜面间的动摩擦因数μ=0.30,BCD是半径为R=0.2m的光滑圆弧轨道,它们相切于B点,C为圆弧轨道的最低点,整个空间存在着竖直向上的匀强电场,场强E=4.0×103N/C,质量m=0.20kg的带电滑块从斜面顶端由静止开始滑下.已知斜面AB对应的高度h=0.24m,滑块带电荷q=-5.0×10-4C,取重力加速度g=10m/s2,sin37°=0.60,cos37°=0.80.求:| h |
| sin37° |
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 2 |
| 1 |
| 2 |
| v | 2 1 |
| ||
| R |


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中物理 来源: 题型:
(12分)为了研究过山车的原理,物理小组提出了下列的设想:取一个与水平方向夹角为37°、长为L=2.0m的粗糙的倾斜轨道AB,通过水平轨道BC与竖直圆轨道相连,出口为水平轨道DE,整个轨道除AB段以外都是光滑的。其中AB与BC轨道以微小圆弧相接,如图所示。一个小物块以初速度![]() ,从某一高处水平抛出,到A点时速度方向恰沿AB方向,并沿倾斜轨道滑下。已知物块与倾斜轨道的动摩擦因数
,从某一高处水平抛出,到A点时速度方向恰沿AB方向,并沿倾斜轨道滑下。已知物块与倾斜轨道的动摩擦因数![]() (g取10m/s2,
(g取10m/s2,![]() )求:
)求:
(1)小物块的抛出点和A点的高度差;
(2)要使小物块不离开轨道,并从水平轨道DE滑出,求竖直圆弧轨道的半径应该满足什么条件;
(3)为了让小物块不离开轨道,并且能够滑回倾 斜轨道AB,则竖直圆轨道的半径应该满足什么条件。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com